A hidden Markov model (HMM) is a statistical Markov model in which the system being modeled is assumed to be a Markov process with unobserved (hidden) states. Hidden Markov models are especially known for their application in temporal pattern recognition such as speech, handwriting, gesture recognition [1], part-of-speech tagging, musical score following [2], partial [3] and bioinformatics. Hidden Markov Chain (HMC) is derived from context mentioned hidden Markov model (HMM).

The entropy rate or source information rate of a stochastic process is, informally, the time density of the average information in a stochastic process and it plays great roles in information theory. Therefore, in recent years, many approaches have been adopted to try to improve theoretical integrity about the entropy rate of a hidden Markov chain. For instance, Ordentlich et al.[4] used Blackwell’s measure to compute the entropy rate and Egner et al.[5] introduced variation bounds. Ordentlich et al.[4], Jacquet et al.[6], Zuk et al.[7] etc studied the variation of the entropy rate as parameters of the underlying Markov chain. Liu et al.[8] have given some limit properties of relative entropy and relative entropy density and Shannon-McMillan theorem for inhomogeneous Markov chains.

Motivated by the work above, the main object of our study is to extend some results mentioned above to HIMC and establish an entropy rate theorem under some mild conditions. For the definitions and methods, we learn from W.G. Yang et al.[9] and G.Q. Yang et al.[10]. W.G. Yang et al.[9] proved a convergence theorem for the Cesaro averages for inhomogeneous Markov chains, gave a limit theorem of one functional of inhomogeneous Markov chains and discussed the application of this limit theorem on the Markovian decision process and the information theory. G.Q. Yang et al.[11] introduced the notion of countable hidden inhomogeneous Markov models, obtained some properties for those Markov models and established two strong laws of large numbers for countable hidden inhomogeneous Markov models and its corollaries.

The remainder of the paper is organized as follows: Section 2 provides a brief description of the HIMC and related Lemmas. Section 3 gives the main results and proofs.

In this section we have some fundamental definitions and related preliminaries that are needed in the next section.

Let ζ = (ξ, η) be random vector, where ξ = (ξ ₀, ξ₁, ···), η= (η ₀,η₁, ···) are two different stochastic processes, η is hidden (η takes values in Y = {ω ₀, ω₁, ···}), and ξ is observable (ξ takes values in set X = {θ ₀, θ₁, ···}).

We first recall the definition of a hidden inhomogeneous Markov chain (HIMC) ζ = (ξ, η) = 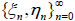with hidden chain 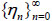and observable process .

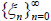Definition 1. [11] The process ζ = (ξ, η) is called an HIMC if it follows the following form and conditions:

1. Assume that a given time inhomogeneous Markov chain takes value in state space Y and its starting distribution be

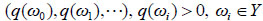(2.1)

and transition matrices

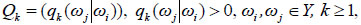(2.2)

Where

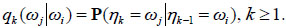2. For any n,

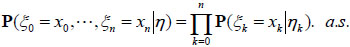(2.3)

Some necessary and sufficient conditions for (2.3) have been proved by G.Q. Yang et al [11].

a. A necessary and sufficient condition for (2.3) holds that for any n, we have

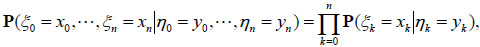(2.4)

b. ζ = (ξ, η) is a inhomogeneous hidden Markov model if and only if 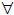n > 0

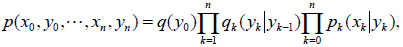(2.5)

c. ζ = (ξ, η) is a inhomogeneous hidden Markov model if and only if 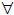n > 0

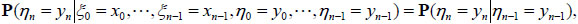(2.6)

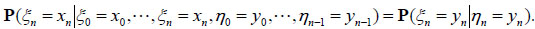(2.7)

Definition 2. Let h = (h ₀, h₁, ···) be a vector, define the norm of h by

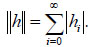Let A = (a_ij) be a square matrix, defining the norm of A by

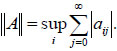Definition 3. [11] Let Q be a transition matrix of a homogeneous Markov chain. We call Q strongly ergodic, if there exists a probability distribution π = (π ₀, π₁, π₂, ···) on Y which satisfies that

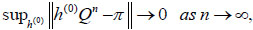(2.8)

where h⁽⁰⁾ is a starting vector, Obviously, (2.8) implies π Q = π, and we call π the stationary distribution determined by Q.

Definition 4. [9] Let 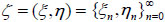be a hidden inhomogeneous Markov chain defined as above and H (ξ₀ , η₀ , ···, ξ_n, η_n) be the entropy of ζ. The entropy rate of ζ is defined by

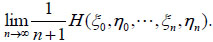For simplicity, we use the natural logarithm here, thus the entropy is measured by NATS. From the definitions of entropy and HIMC, we have

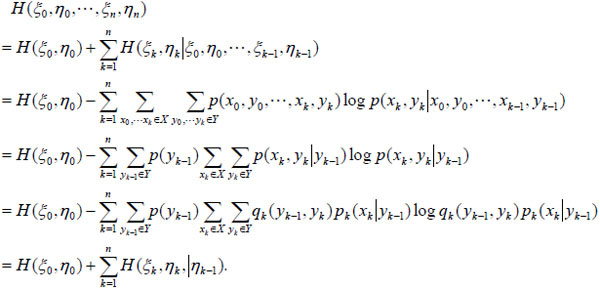Lemma 1. [10] Let η = (η ₀, η₁, ···) be an inhomogeneous Markov chain with transition matrices {Q_n, n≥1}. Let Q be a periodic strong ergodic random matrix. Let c= (c₁, c₂, ···) be a left eigenvector of Q and the unique solution of equations cQ = c and ∑_jc_j= 1. Let B be a constant random matrix, where each row of B is c. If

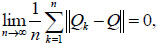(2.9)

then

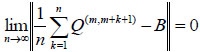(2.10)

holds for any m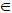 N, where 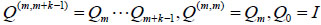(I is the identical matrix).

Lemma 2.Let {g_n, n ≥ 1} and g be column vectors with real number entries, if

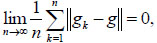(2.11)

then there exists a subsequence {g_nk, k ≥ 1} of {g_n, n ≥ 1} such that

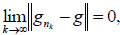(2.12)

Proof. Assume (2.11) holds, We have

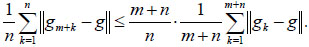(2.13)

Hence

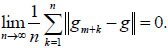(2.14)

holds for any m 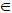N.

choose X_k > 0 with X_k ↓ 0, by (2.14), 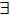M 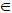N , such that

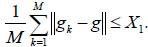(2.15)

Therefore, there exists n₁ ≤ M such that ||g_n1−g|| ≤ X₁, by eq. (2.14), we have

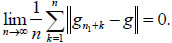(2.16)

Therefore, there exists n₂ ≥ n₁ such that ||g_n2−g|| ≤ X₂. Generally, we can get a subsequence {g_nk, k ≥ 1} of {g_n, n ≥ 1} such that || g_nk − g || ≤ X_k. (2.12) follows immediately.

Theorem 1.Let 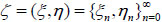be an HIMC defined as above, Q = (q(ω_i, ω_j)) be another transition matrix and assume that Q is periodic strongly ergodic. Let

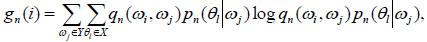(3.1)

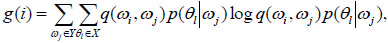(3.2)

where, g_n (i), g(i) are the i th-coordinate of column vectors g_n and g resp., {||g_n||, n ≥ 1} are bounded. If

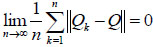(3.3)

and

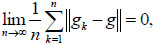(3.4)

then the entropy rate of ζ =(ξ, η) exists and

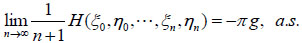(3.5)

where, π = (π ₀, π₁, π₂···) is the unique stationary distribution determined by Q.

Proof. Let h^(k−1) be a row vector with the ith coordinate P (η_k−1 = ω_i). Hence, using the properties and the definition of g_k, we have

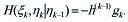(3.6)

Just take B to be a constant random matrix whose rows are equal to π. Note that π = h⁽⁰⁾B, where h⁽⁰⁾ is a starting distribution of the Markov chain. Since

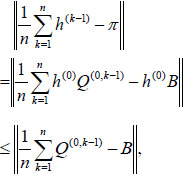(3.7)

where, Q^{(0, k−1)} = Q₁···Q_k−1, Q^{(0, 0)} = I (I is the identical matrix), By Eqs. (3.3) and (3.7) and

Lemma 1, we have

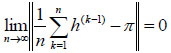(3.8)

By Eq. (3.4) and Lemma 2, there exists a subsequence 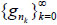of 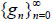such that

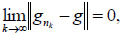(3.9)

hence ||g|| is finite. By Eq. (3.8) and the entropy property, we have

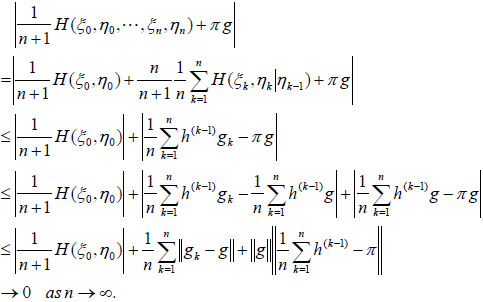This completes the proof of Theorem 1.

Remark. Theorem 1 gives a method to compute the entropy rate of an HIMC under some mild conditions.

Corollary 1.Let 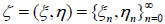be a hidden homogeneous Markov chain with periodic strongly ergodic transition matrix Q(q(ω_i, ω_j)) and transition probability p(θ_l|ω_j), where ω_i, ω_j 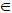Y, θ_l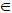 X. Let

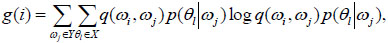(3.10)

where, g(i) is the i th-coordinate of column vectors g, ||g|| is bounded. Then the entropy rate ofζ = (ξ, η) exists and

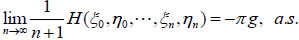(3.11)

where, π = (π ₀, π₁, π₂···) is the unique stationary distribution determined by Q.

As a corollary we can get the following theorem of W.G. Yang et al.[9] for an inhomogeneous Markov chain.

Corollary 2. [9] Let 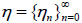be an inhomogeneous Markov chain, Q = (q(ω_i, ω_j)) be another transition matrix and assume that Q is periodic strongly ergodic. Let

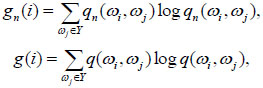where, g_n(i), g(i) are the i th-coordinate of column vectors g_n and g resp., {||g_n||, n≥1} are bounded. If

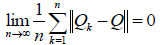and

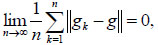then the entropy rate of η exists and

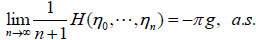where, π = (π ₀, π₁, π₂···) is the unique stationary distribution determined by Q.

We quote the definition of HIMC, norm, stationary distribution and entropy rate which contain rich content. Lemma 1 gives a limit property of state transition matrices of an inhomogeneous Markov chain. Lemma 2 gives a limit property of vector series. The process of proof references the situation of inhomogeneous Markov chains. Key to the proof is that Cesaro average of state distribution of a Markov chain takes stationary distribution as the limit. Under some mild conditions, the entropy rates of an inhomogeneous Markov chain, a hidden Markov chains and a HIMC are similar and easy to calculate.