Record values are found in many real lifetime datasets such as observing new records in k-th highest or k-th lowest values of weather-conditions, temperatures, water-levels, Olympic or world records in sports. In addition, record values are used in theory of reliability. Furthermore, these statistics are related to the occurrence times of some non-homogenous Poisson process used in shock models Kamps [1]. Chandler [2] started the statistical study of record values as a model considering dependence structure for successive extremes in a sequence of independent and identically distributed (iid) random variable. This means that, the life-length distribution of system components may change after the failure of each component. Dziubdziela and Kopocinski [3] proposed the limiting distribution of k-th record values where k is some positive integer. Many authors have considered characterization of distributions through conditional expectation of record values, for instance, Nagaraja [4], Franco and Ruiz [5, 6], Khan and Alzaid [7], Khan, Faizan, and Haque [8], and Lopez-Blazques and Moreno-Rebollo [9]. For more information in the theory of records and its distributional properties and some characterizations of k-th record values can be found in, for example, Ahsanullah [10, 11], Arnold, Balakrishnan, and Nagaraja [12], Nevzorov [13], Deheuvels [14], Nagaraja [15], Raqab and Awad [16] and references therein.

Let {X_i, i ≥ 1} be a sequence of independently and identically distributed (iid) random variables with cumulative distribution function (cdf)F(x) and probability density function (pdf)f(x). For a fixed k ≥ 1, the kth lower record value of X'_i s is defiend by:

Note  that with

are lower record values.

For

we have the following (see Ahsanullah [10, 11], Arnold, Balakrishnan, and Nagaraja [12], Nevzorov [13]:

The pdf of Z_r^(k) and (Z_r^(k), Z_s^(k)) are as follows:

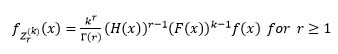(1)

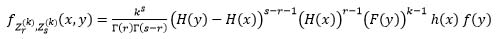(2)

We shall denote:

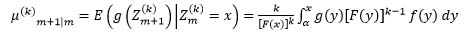(3)

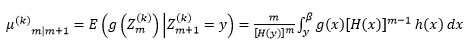(4)

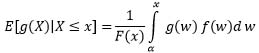(5)

Such that g is a continuous, monotonic and differentiable function on (α,β).

In this paper, we present three general classes of distributions whose cdf’s are:

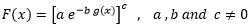(6)

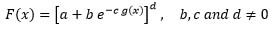(7)

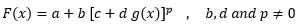(8)

such that g is a continuous, monotonic and differentiable function on (α,β).

We extend using the cdf in (6) some work of Al-Shomrani and Shawky [17] as shown in Theorem 1 by characterizing this first general form of distributions through conditional expectation of p-th power of difference of functions of two k-th lower record values. Moreover, Theorems 2.5 and 2.6 in Shawky and Abu-Zinadah [18] and Theorems 3 and 4 in Shawky and Bakoban [19] are generalized as shown in Theorems 2 and 3 using the cdf in (7) by characterizing the second general class of distributions through conditional expectation of k-th lower record values. Lastly, we show that equation (2.1.1) in Hamedani, Javanshiri, Maadooliat, and Yazdani [20] is a special case of Theorem 4 by using the cdf in (8) as the third general class of distributions based on truncated moments of some random variable. Some distributions as members of these general classes are given as examples in Tables 1 and 2.

Theorem 1:

Let X be an absolutely continuous random variable with cdf F(x) and pdf f(x) on the support (α,β), F(α) = 0 and F(β) = 1. Then, for two values of r and s, 1 ≤ r < s ≤ n (where 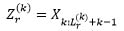as defined above).

Table 1. Examples of (7).

Distribution	F(x)	g(x)	a	b	c	d
Weibull		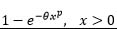xp	1	-1	θ	1
Pareto of the first kind		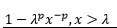lnx	1	-λp	p	1
Burr XII		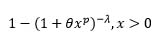ln (1+θxp)	1	-1	λ	1
Rayleigh		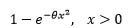x2	1	-1	θ	1
Lomax		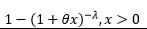ln (1+θx)	1	-1	λ	1
Inverse Weibull		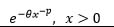x-p	0	1	θ	1
Power function		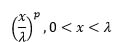	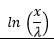0	1	-p	1
Rectangular		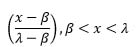ln(x-β)	0		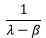-1	1
Pareto of the second kind		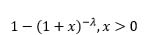ln (1+x)	1	-1	λ	1
Exponential		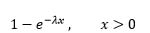x	1	-1	λ	1
Inverse Exponential		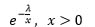	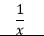0	1	λ	1
Kumaraswamy		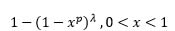ln (1-xp)	1	-1	-λ	1
Exponentiated Frechet		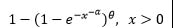	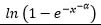1	-1	-θ	1
Exponentiated exponential		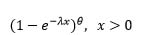ln (1-e -λx)	0	1	-θ	1
Burr X (Exponentiated Rayleigh)		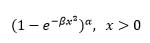x2	1	-1	β	α
Exponentiated Weibull		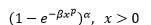xp	1	-1	β	α

Table 2. Examples of (8).

Distribution	F(x)	g(x)	a	b	c	d	p
Weibull		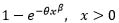	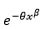0	1	1	-1	1
Pareto of the first kind		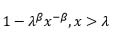	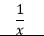1	-1	0	λ	β
Burr XII		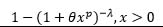xp	1	-1	1	θ	-λ
Rayleigh		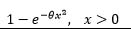	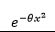0	1	1	-1	1
Lindley		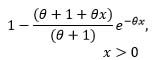	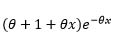1		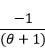0	1	1
Lomax		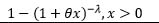x	1	-1	1	θ	-λ
Dagum		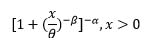x-β	0	1	1	θβ	-α
Pareto of the second kind		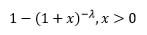x	1	-1	1	1	-λ
Exponential		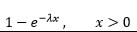ex	0	1	1	-1	-λ
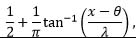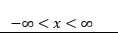
Cauchy					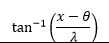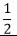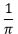0	1	1
Kumaraswamy		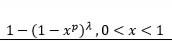xp	1	-1	1	-1	λ
Exponentiated Gumbel		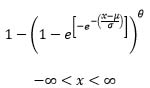	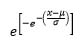1	-1	1	-1	θ
Exponentiated power Lindley		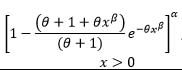	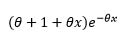0	1	1		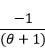α

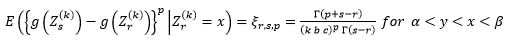(9)

if and only if:

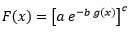
Where g(x) is a continuous, differentiable and non-decreasing function of x and p is a positive integer.

Proof:

For proving the necessary part, from (1) and (2), we have for s≥ r+1:

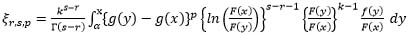(10)

Using (6), suppose,

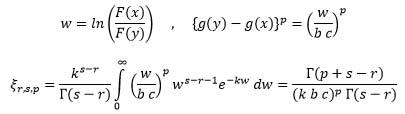
Hence the necessary part is proven.

For the sufficiency part, it is clear from (10) that:

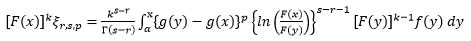(11)

Differentiating both sides in (11) with respect to x, we get:

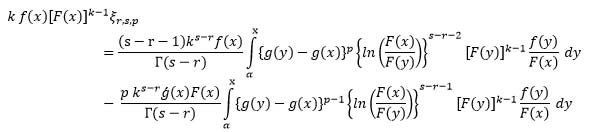
Using (10), we can get that:

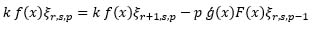
and from (9),

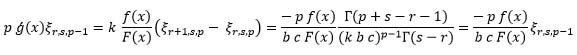
which gives:

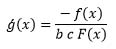
Therefore, the proof is completed.

Theorem 2:

Let X be an absolutely continuous random variables with distribution function F(x) and xϵ (α,β), F(α) = 0 and F(β) = 1, then:

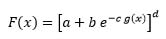
if and only if:

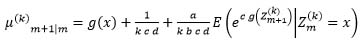(12)

Where b, c and d ≠ 0 are finite constants and g(x) is a continuous, monotonic and differentiable of x on the support (α,β).

Proof:

Proving the necessary part, in view of (3), we can get:

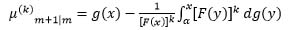(13)

Now, from (7), we obtain:

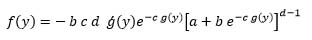
which gives:

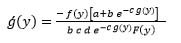(14)

Substituting (14) into (13), we get:

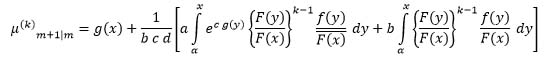
Therefore, (12) is obtained.

For proving the sufficiency part, from (12) and (13), we obtain:

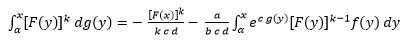(15)

Differentiating both sides in (15) with respect to x, we get:

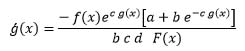
Hence, the proof is completed.

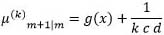Theorem 3:

If F(x) < 1 be any cdf of the continuous random variable X and xϵ (α,β), F(α) = 0 and F(β) = 1, then:

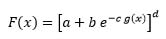
if and only if,

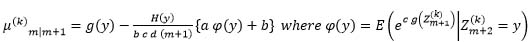(16)

Where b, c and d ≠ 0 are finite constants and g(x) is a continuous, monotonic and differentiable of x on the support (α,β).

Proof:

For the necessary part, in view of (4), it is straightforward to get:

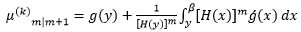(17)

Substituting (14) into (17) result in:

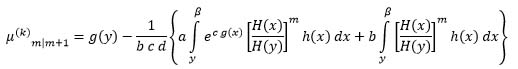
this completes the necessary part.

For the sufficiency part, we have from (16) and (17) that:

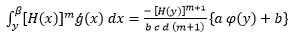(18)

From (16), we get,

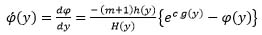(19)

Differentiating both sides in (18) with respect to y and substituting (19), we have:

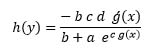
hence, the theorem is proved.

Theorem 4:

Referring to (5) and (8), then:

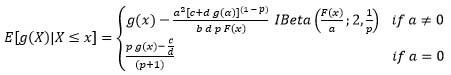(20)

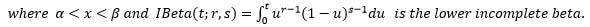
Proof:

If a ≠ 0 and from (5) and using integration by parts, we get,

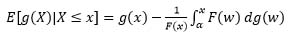(21)

Now, using (8), we have:

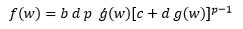
this implies,

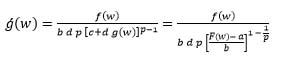(22)

Substituting (22) into (21), we get:

Let , then

Where

Let u = 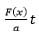, then

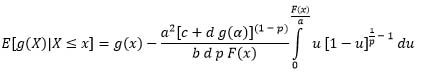
Therefore, the upper part of (20) is achieved.

If a = 0 and from (21) and (22) then,

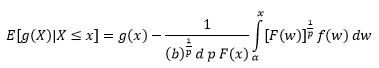
Let 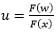, then

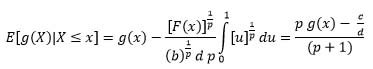
Thus, the lower part of (20) is achieved.

Remark:

The RHS of equation (20) where a = 0 is the same as that of equation (2.1.1) in Hamedani, Javanshiri, Maadooliat, and Yazdani [20].

In this study some characterization results and recurrence relations of certain distributions based on the k-th lower record values for three general classes are obtained. Firstly, we characterize the first general form of distributions through conditional expectation of p-th power of difference of functions of two k-th lower record values as shown in Theorem 1. Secondly, two Theorems 2 and 3 are presented for two recurrence relations of the second general class of distributions through conditional expectation of k-th lower record values. Thirdly, we establish an expression of conditional expectation for the third general class of distributions based on truncated moments of some random variable as shown in Theorem 4. Finally, we show examples of some distributions related to these general classes as in Tables 1 and 2.