RESEARCH ARTICLE


Analysis of Stable Targets in High-Resolution Polarimetric SAR Data Stacks



B. Scheuchl*
University of California, Irvine, CA 92697, USA

Article Information


Identifiers and Pagination:

Year: 2016
Volume: 7
First Page: 10
Last Page: 19
Publisher Id: TOSPJ-7-10
DOI: 10.2174/1876527001607010010

Article History:

Received Date: 27/4/2015
Revision Received Date: 24/7/2015
Acceptance Date: 4/4/2016
Electronic publication date: 23/06/2016
Collection year: 2016

© B. Scheuchl; Licensee Bentham Open.

open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution-Non-Commercial 4.0 International Public License (CC BY-NC 4.0) (https://creativecommons.org/licenses/by-nc/4.0/legalcode), which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.

Correspondence: Address correspondence to this author at the University of California, Irvine, CA 92697, USA; E-mail: bscheuch@uci.edu


Abstract

Polarimetric SAR data provide information about the scattering of the area observed. The availability of data stacks allows the identification of stable targets and subsequent scattering analysis with a high degree of confidence at full resolution. A novel approach to find and evaluate polarimetric persistent target is presented, that is an extension of well-established analysis methods for single scenes. The use of the Cloude-Pottier distributed target decomposition analysis applied on the temporal averages (as opposed to spatial averaging), combined with a Cameron point target analysis applied on each layer separately to select pixels only, provides an efficient scattering classification of polarimetric persistent point targets in the stack. This method can also be used to analyze targets identified through other means, albeit at a lower degree of confidence. The approach retains the full resolution of the data set, though temporal changes between acquisitions add additional complexity. Result interpretation is therefore performed under consideration of a set of boundary conditions. Results from the analysis of two polarimetric data stacks acquired by RADARSAT-2 are shown.

Keywords: Data stack, Entropy, Polarimetric persistence, SAR polarimetry, Target decomposition, Time series.

1. INTRODUCTION

The analysis of SAR time series data (or data stacks) comprised of multiple scenes (n > 15) was first introduced through the development of PS-INSAR analysis [1]. Single polarization data stacks from the European ERS-1/2 missions were readily available and greatly aided method development. Few second-generation SAR satellites are capable of collecting polarimetric data operationally, so there are not many polarimetric SAR data stacks available to date. As a consequence, the analysis of polarimetric time series data is not wide spread. Cloude et al. investigate time series decomposition analysis for compact polarimetry and employ a mixed space/time average to help reduce speckle and highlight key land-use features [2]. Conradsen et al. present an improved method to analyze polarimetric time series data for changes instead of pairwise investigation of the data [3]. The concept of point-like coherent scatterers in urban areas is introduced in [4]. The authors investigate airborne L-band high-resolution data for interferometric and polarimetric properties, but only have a short time series available (3 scenes). An approach to utilize polarimetric time series data for land cover monitoring is presented in [5]. The authors perform traditional polarimetric analysis methods on a per acquisition basis.

Here, a novel way to evaluate polarimetric persistent point targets in data stacks is presented. The approach is an extension of a traditional method to analyze distributed targets that is used under consideration of a set of restrictions. For improved accuracy, the method is combined with acoherent decomposition applied to select targets only. Tests on two polarimetric data stacks acquired by RADARSAT-2 were performed.

2. BACKGROUND

A number of methods were developed that allow the decomposition of polarimetric data for a more detailed characterization of the scattering.

2.1. Point Target Analysis (Coherent Decomposition)

Coherent target decomposition methods express the scattering matrix, S, a single look expression of polarimetric data, as a combination of scattering responses of simpler objects [6].

  1. Cameron Decomposition Using a factorization of S based on reciprocity and symmetry, a normalized complex quantity, z, is extracted from the data and is subsequently used to classify the scattering matrix into one of 6 classes based on the distance (in a unit disc) to pure canonical targets (i.e. trihedral, cylinder, dipole, narrow diplane, dihedral, and quarter wave) [7].
  2. Symmetric Scattering Classification Method (SSCM) Touzi and Charbonneau extend the Cameron method to SSCM by extending the observation space from a 2D plane to one half of the Target Poincare sphere [8]. The authors claim that their method represents a refinement of the Cameron decomposition, though the elemental scatterers that define the type interpretation are the same. Cameron et al. [9] suggest that an ambiguity persists in SSCM. Giusti et al. [10] show the mathematical equivalency of the original Cameron unit disk method with the Poincare method.
  3. Other Point Target Analysis Methods Other methods include Huynen, Pauli, and Kroager [11]; they are not included in this study.
Table 1.

RADARSAT-2 polarimetric data stacks.


Montreal Vancouver
Mode FQ16 FQ2
Incidence angle 36° 21°
Number of Scenes 15 44
Observation start January 2011 April 2008
Observation end February 2012 February 2012
Pixel spacing azimuth 5.1m 5.1m
Pixel spacing range 4.7m 4.7m

2.2. Distributed Target Analysis (Incoherent Decomposition)

Distributed targets are described statistically because of the presence of speckle. Second order polarimetric representations like the coherency matrix, T, can be spatially averaged to reduce the effect of speckle [6]. One widely used method to analyze distributed polarimetric targets is the Cloude-Pottier decomposition [12]. Three main parameters are generated from the decomposition of the averaged coherency matrix in eigenvectors and eigenvalues: the Entropy, H, which determines the randomness of the scattering, the Anisotropy, A, which relates the two smaller eigenvalues, and the α- angle, which describes the average dominant scattering mechanism.

2.3. Model-based Target Analysis

Model based target analysis methods like Van Zyl [13], Freeman/Durden [14], or Yamagucci [15] were developed specifically for distributed targets. These methods are not considered in this study and are mentioned for completeness only.

3. DATA

Two RADARSAT-2 Fine-Quad (FQ) data stacks were available for this study and are described in Table 1. To facilitate time series analysis, all scenes for each of the stacks were co-registered to a common master with sub-pixel accuracy. Only sub-images were investigated for both stacks for easier data handling. Due to the larger stack size, a smaller spatial subset was processed for the Vancouver data set to reduce the size of the data set.

4. ANALYSIS OF POLARIMETRIC DATA STACKS

Four guiding principles in the development of a method for the analysis of point targets in polarimetric data stacks can be defined:

  • Coherent target decomposition methods used on polarimetric data stacks need to be used on each level separately.
  • Distributed target analysis methods can be applied to data averaged through time thus preserving resolution.
  • The temporal component of a data stack adds a level of complexity to the interpretation of the analysis results.
  • This work focuses on stable targets only. No attempt is made to interpret changes between acquisitions.

Using these guidelines, three methods to derive information from the polarimetric data stack for the purpose of identifying and analyzing stable polarimetric targets were used.

  1. Implementation of the Touzi criterion [8] to identify coherent targets for each layer of the stack separately.
  2. Stack Cameron Decomposition. Implementation of the Cameron decomposition and application on each layer of the data stack separately resulting in a stack of Cameron classes. (SSCM was implemented in a similar fashion, but given the similarity of the methods this avenue was not further investigated.)
  3. Calculate the time average coherency matrix T3average through the stack for each pixel (x,y). Based on T3average, calculate Hstack, Astack, and αstack for the time-averaged data. These parameters retain the resolution of the original data. Because the focus here is on targets with one dominant scattering mechanism, Astack for these points is based on small values and likely strongly affected by noise. Astack is therefore not used for result interpretation.
The implementation described above leads to three different results that require careful interpretation. Interferometric analysis of data stacks for the evaluation of target displacement requires a careful selection of target candidates that meet certain criteria [16]. The same concept is true when looking at polarimetric analysis of a data stack for the purpose of target identification, though a different set of criteria needs to be met. Here, we define Polarimetric Persistence, which essentially requires a level of consistency of analysis results through the data stack:

4.1. Consistent Identification as a Coherent Target

A pixel is polarimetric persistent in the Touzi criterion [8] sense if the number of times (layers) a pixel is identified as coherent polarimetric point target exceeds a confidence threshold. A 70% threshold (or more than 2/3rds of layers) was chosen, but tests were also undertaken with 80%, 90%, and 100% thresholds. Note that for this criterion the target type is not identified.

4.2. Consistent Cameron Class Through the Data Stack

A pixel is polarimetric persistent in the Cameron class sense if the number of layers with the same class meets or exceeds a confidence threshold. Again, a 70% threshold (or more than 2/3rds of layers) was selected, but tests were also undertaken with 80%, 90%, and 100% thresholds.

4.3. Low HStack

Based on [12], low Entropy (H<0.5) indicates a single dominant scatterer for a spatially averaged resolution element. The same principle holds true for a time averaged resolution element. A single dominant scatterer in a resolution element with little to no change within the pixel throughout the observation period will result in low Hstack. This subsequently allows an interpretation of the αstack-angle to describe the average dominant scattering mechanism based on the principles derived in [12]. Note that the αstack-angle for higher Entropies, Hstack, is very likely (but not necessarily) affected by change between the multiple acquisitions and should therefore not be interpreted without additional information at hand.

Polarimetric persistence can be used to identify targets in the data stack for further analysis. It can also provide a measure of confidence in the interpretation of targets that were selected through different means. Of the three methods mentioned above, Hstack provides the most efficient means for target selection.

Both αstack-angle and the stack Cameron class results provide information for target interpretation. The latter provides distinct classes, but is less computationally efficient. Using a combined approach, the two methods can be used according to their strengths. Hstack/αstack provides a fast pre-selection and allows initial interpretation. The stack Cameron method subsequently needs to be applied on pre-selected points only, leading to a more efficient use with increased confidence in the result. Fig. (1) shows the flow diagram of the algorithm as implemented.

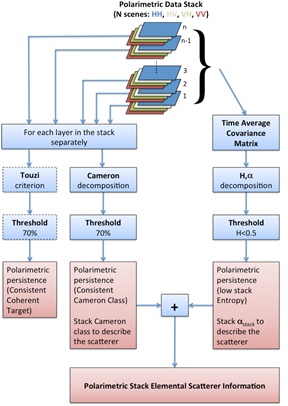Fig. (1).

Flow diagram of the proposed approach.

5. RESULTS AND DISCUSSION

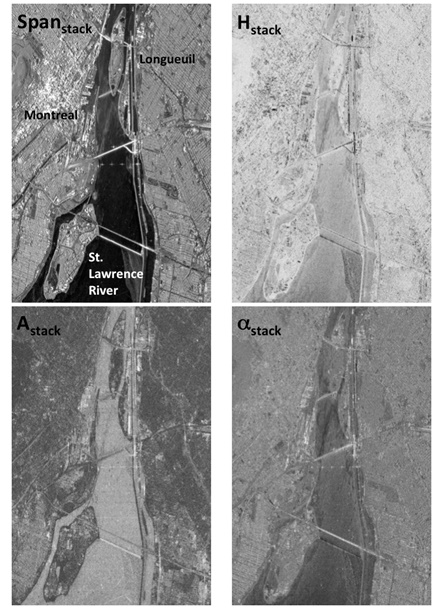
Fig. (2) shows the time averaged span image, Hstack, Astack, and αstack for a subset of the FQ Montreal data set. The span image is presented for reference only, to allow easier interpretation of the other parameters. The scene shows generally high Entropy. This is also evident in the color density scatter plot of the Hstack,αstack-space (Fig. (3), top image). Similar to spatially averaging Entropy, Hstack represents a mix of scattering mechanisms in the resolution element; however, here the mixing occurs on two levels: 1) spatially, within the resolution element, and 2) temporally, through changes between the acquisitions of the data stack. This second dimension of change renders high entropy pixels ambiguous and unsuitable for a detailed polarimetric analysis through the data stack, unless additional information is available. Therefore, we focus here on low entropy portions of the scene. Of particular interest are areas with Hstack<0.5. Lower Hstack means that the pixel can be interpreted with higher confidence.

It should be noted that a stable target can result in high Hstack. Such a target will have multiple scattering mechanisms within the resolution cell equally contributing to the final signal. The proposed threshold will therefore not catch all stable targets, but pure ones.

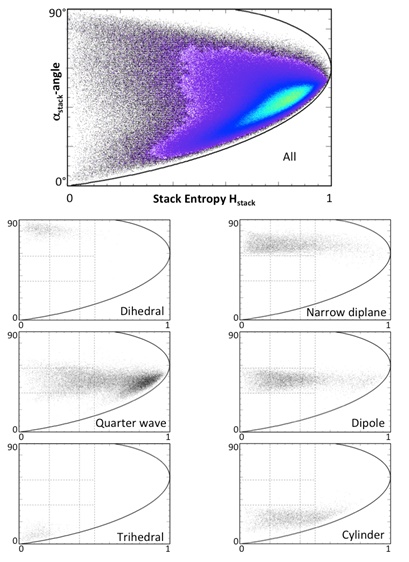
Fig. (3) (lower 6 plots) shows a comparison of the stack Cameron class results and the Hstack, αstack-space (a confidence threshold of 70% was chosen for this case, i.e. the same Cameron result was obtained in more than 70% of layers). Each stack Cameron class is presented in a separate plot. The plots clearly show the relation between each stack Cameron class and the αstack-angle. Both decompositions describe the scattering type of the resolution element and, more importantly, both provide the same information. Dihedral and Trihedral scattering are well separated (αstack~90° and αstack~0° respectively, with about 10° range) and consistent with the definition of the α-angle for a single scene. Low αstack is equated with rough surface scattering (single bounce). A Trihedral (triple bounce) shows the same polarimetric behavior as a single bounce return, except for the backscatter strength. Narrow Diplane (αstack > 57.5°) scattering is more closely related to dihedral scattering than it is to trihedral scattering. Dipole scattering shows α-angles between 35° and 57.5°. Quarter wave scattering also roughly lies in this center band, although higher Hstack values can be observed for the latter case. Cylinder scattering is best described with αstack-angles smaller than 35°. While there are exceptions, particularly noted are the quarter wave results, the majority of the stack Cameron results show a low Hstack. The vast majority of stable targets identified using the Touzi criterion also show Hstack<0.5. Higher confidence thresholds for stack Cameron and the Touzi criterion lead to fewer points identified in both cases that also show a lower average Hstack. The plots for the Vancouver data set (see Fig. 4) are consistent with the Montreal results. These results are in agreement with the hypothesis that time averaged entropy for a pixel can be interpreted as an indication of a stable target for the data stack.

Fig. (2).

Montreal data set stack averaged span, Hstack and Astack (black=0, white=1), as well as αstack (black=0 degrees, white=90 degrees). The scene encompasses downtown Montreal (on the top left of the scene) with surroundings, the St. Lawrence River, and several bridges.

Fig. (3).

Hstack/αstack density scatter plot of the Montreal data stack (black=low density to yellow=high densitly; top image). Cameron stack results with a 70% confidence threshold are plotted in the Hstack/αstack space (rest).

Fig. (5) shows the classification result of the combined approach for the Montreal scene. Only polarimetric persistent points are classified into elemental scatterers. A more detailed view is shown in Fig. (6). Classified targets are predominantly located in the downtown core and in other built up areas. This is to be expected as these areas have a high likelihood for point targets.

One potential application of the method is the classification of point targets identified using other means. A method to identify persistent targets in the InSAR sense (PTIn) is to select them using the phase stability method [16]. The approach seeks to identify targets with a stable interferometric phase in a single-polarization data stack for PS-INSAR analysis. Target characterization is not provided. If a polarimetric data stack is available, the method proposed here can be used for providing information about the type of pure elemental scatterers with high confidence. Hstack, αstack decomposition and stack based Cameron decomposition can also be used to provide polarimetric information for all PTIn. In this case the detection is provided through the phase stability method only. Hstack and/or the number of scenes with consistent Cameron class provide a measure for the classification confidence, instead of being used for detection.

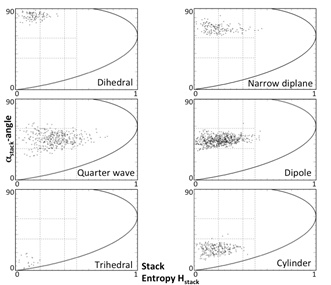Fig. (4).

Hstack/αstack scatter plot of the Vancouver data stack. Cameron stack results with a 70% confidence threshold are plotted in the Hstack/αstack space.

For the Montreal data set, about 20% of PTIn in the scene are directly classified with the proposed method. The difference is likely because PTIn are selected based on phase stability only, a criterion which can be satisfied for pure targets as well as for targets with a mix of scatterers. Polarimetric persistent targets are pure targets by definition, which requires a single dominant scattering mechanism.

In comparison, for the Vancouver data set, only 6.2% of PTIn are directly classified using the proposed method (see Fig. 7). This lower number is likely due to the steeper incidence angle for the acquisitions. The resulting lower ground range resolution leads to a larger area covered by a pixel. This leads to a higher potential for more scattering mix in a single resolution cell.

For both data sets, all PTIn can be interpreted as discussed above. The confidence in the classification result will be lower, as these points likely experience a greater degree of scattering mix, which means targets are no longer pure. The resulting stack entropy serves as an indicator of the classification confidence. The stable phase of the PTIn indicates little change over time and the time average coherency matrix can in fact be used to interpret the target. The interpretation of αstack is similar to the original interpretation suggested in [12], indicating an average dominant scattering mechanism, whereas Hstack describes the scattering mix.

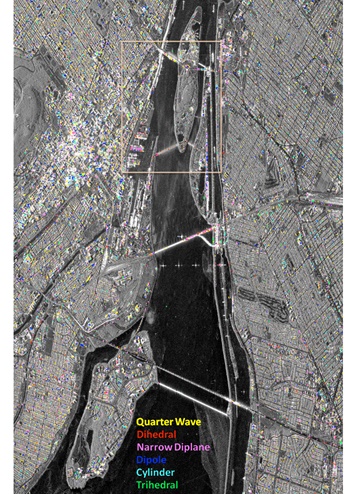Fig. (5).

Combined Hstack/αstack - stack Cameron classification of the Montreal data stack overlaid on the time averaged span image. The inset shows the detail presented in Fig. (6).

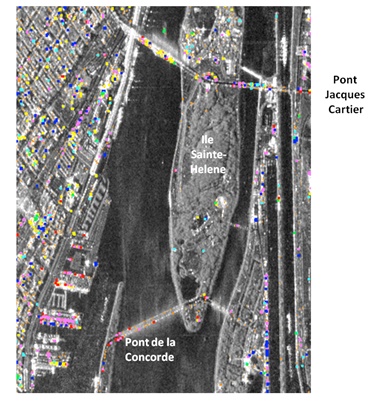Fig. (6).

Detail of the combined Hstack/αstack - stack Cameron classification presented in Fig. (5). Orange points indicate unclassified PTIn.

SUMMARY AND CONCLUSION

A novel way to find and evaluate stable targets in polarimetric SAR data stacks is introduced. The approach is an extension of well-established polarimetric analysis methods for single scenes. It retains the full resolution of the data set, though temporal changes between acquisitions add additional complexity. Result interpretation is therefore performed under consideration of a set of boundary conditions.

Traditional point target analysis methods like the Cameron decomposition allow a rigorous evaluation of polarimetric point targets; however, they need to be applied on every layer of a polarimetric data stack separately. Proof is provided that distributed target decomposition methods can be applied on a data stack while preserving resolution. The proposed Hstack, αstack analysis allows a fast and reliable identification and evaluation of stable targets in polarimetric data stacks. Hstack can be used to identify polarimetric persistent scatterers. It can also be used as a degree of confidence in the subsequent analysis. The αstack–angle describes the type of scatterer; its output for polarimetric persistent targets is consistent with stack Cameron results. The recommended thresholds for the αstack-angle are driven by a comparison with the stack Cameron results.

  • αstack < 35°: Trihedral scattering (α~0°, with a 10° band) or cylinder scattering (rest). A clear separation of these two scattering types solely based on αstack is not possible with a simple threshold, though trends can be observed.
  • 35° < αstack < 57.5°: Dipole or quarter wave scattering (further separation not possible solely in the Hstack/αstack-space)
  • αstack > 57.5°: double bounce scattering (αstack~90°, with a 10 ° band), or narrow diplane scattering (rest)

The proposed approach uses the Hstack, αstack method in combination with a stack Cameron decomposition (the latter can be used more efficiently on select points only). The result is a classification of polarimetric stable points in a scene to pure canonical targets (i.e. trihedral, cylinder, dipole, narrow diplane, dihedral, quarter wave, and helix) with a high degree of confidence.

Fig. (7).

Vancouver data set stack averaged span, Hstack (black=0, white=1), as well as αstack (black=0 degrees, white=90 degrees). The scene shows a portion of downtown Vancouver and the False Creek region. The Hstack/αstack - stack Cameron classification is shown overlaid on the time averaged span image. Unclassified PTIn are shown in orange.

The polarimetric persistence criteria lead to the identification of fewer points compared to persistent interferometric points. The percentage of persistent interferometric scatterers that also meet the proposed polarimetric persistence criteria appears to be dependent on the incidence angle, with more overlap for shallower incidence angles (with corresponding higher ground range resolution).

The proposed method can also be used to interpret targets identified through other means (like interferometric persistence) and provide a measure of confidence for the analysis results; however, interpretation uncertainties will increase in this case. For targets with high stack Entropy, it is better to interpret αstack as is recommended for distributed targets.

Polarimetric data stacks will likely remain rare given that SAR satellites like RADARSAT-2 have many possible acquisition modes and users may often prefer higher resolution or larger area coverage at single or dual polarization over polarimetric data. This work shows the potential of polarimetric data stacks for the identification and interpretation of targets that meet polarimetric persistence criteria.

CONFLICT OF INTEREST

The author confirms that this article content has no conflict of interest.

ACKNOWLEDGEMENTS

The author would like to thank Parwant Ghuman for numerous fruitful discussions on the topic as well as for providing co-registered data stacks and a list of PTIn, two anonymous reviewers for their valuable feedback that contributed to an improved manuscript, and Aimée Gibbons for proofreading. This work was supported by 3vGeomatics under contract with the Canadian Space Agency’s EOADP program. RADARSAT-2 polarimetric data stacks were provided by MDA through CSA's GOV allocation.

RADARSAT-2 Data and Products© MacDONALD, DETTWILER AND ASSOCIATES LTD. (2012) - All Rights Reserved. RADARSAT is an official mark of the Canadian Space Agency.

REFERENCES

[1] Ferretti A, Prati C, Rocca F. Permanent scatterers in SAR interferometry. IEEE Trans Geosci Rem Sens 2001; 39(1): 8-20.
[2] Cloude SR, Goodenough DG, Chen H, Leckie D, Hill D. Time series decomposition analysis for compact polarimetry. In: Proceedings of PolInSAR. Frascati, Italy: European Space Agency: 6th International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry 2013.
[3] Conradsen K, Nielsen AA, Skriver H. Change detection in a time series of polarimetric SAR data. In: Proceedings of PolInSAR, 7th International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry; Frascati, Italy: European Space Agency. 2015.
[4] Schneider RZ, Papathanassiou KP, Hajnsek I, Moreira A. Polarimetric and interferometric characterization of coherent scatterers in urban areas. IEEE Trans Geosci Rem Sens 2006; 44(4): 971-84.
[5] Cable JW, Kovacs JM, Shang J, Jiao X. Multi-temporal polarimetric RADARSAT-2 for land cover monitoring in northeastern ontario, Canada. Remote Sens 2014; 6(3): 2372-92.
[6] The Polarimetric SAR Data Processing and Educational Tool, Polarimetry Tutorial Part I, Section 4 Polarimetric Decompositions: Available from: http://earth.eo.esa.int/polsarpro/Manuals/4_Polarimetric_Decompositions.pdf [[accessed June 2015].];
[7] Cameron WL, Youssef NN, Leung LK. Simulated polarimetric signatures of primitive geometrical shapes. IEEE Trans Geosci Rem Sens 1996; 34(3): 793-803.
[8] Touzi R, Charbonneau F. Characterization of target symmetric scattering using polarimetric SARs. IEEE Trans Geosci Rem Sens 2002; 40(11): 2507-16.
[9] Cameron WL, Rais H. Conservative polarimetric scatterers and their role in incorrect extensions of the cameron decomposition. IEEE Trans Geosci Rem Sens 2006; 44(12): 3506-16.
[10] Giusti E, Martorella M, Petronio C, Berizzi F. Equivalence between cameron’s unit disc and poincaré’s sphere for symmetric scattering characterization and classification. IEEE Geosci Remote Sens Lett 2008; 5(2): 152-6.
[11] Cloude SR, Pottier E. A review of target decomposition theorems in radar polarimetry. IEEE Trans Geosci Rem Sens 1996; 34(2): 498-518.
[12] Cloude SR, Pottier E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans Geosci Rem Sens 1997; 35(1): 68-78.
[13] van Zyl JJ. Unsupervised classification of scattering mechanisms using radar polarimetry data. IEEE Trans Geosci Rem Sens 1989; 27(1): 36-45.
[14] Freeman T, Durden SL. A three-component scattering model for polarimetric SAR data. IEEE Trans Geosci Rem Sens 1998; 36(3): 963-73.
[15] Yamaguchi Y, Moriyama T, Ishido M, Yamada H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans Geosci Rem Sens 2005; 43(8): 1699-706.
[16] Hooper A, Zebker H, Segall P, Kampes B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys Res Lett 2014; 31: L23611.