RESEARCH ARTICLE


On The Distribution of Partial Sums of Randomly Weighted Powers of Uniform Spacings



Emad-Eldin A. A. Aly1, *
1 Department of Statistics & Operations Research, Faculty of Science, Kuwait University, Safat 13060, Kuwait

Article Information


Identifiers and Pagination:

Year: 2020
Volume: 10
First Page: 1
Last Page: 7
Publisher Id: TOSPJ-10-1
DOI: 10.2174/1876527002010010001

Article History:

Received Date: 02/02/2019
Revision Received Date: 06/11/2019
Acceptance Date: 16/11/2019
Electronic publication date: 14/02/2020
Collection year: 2020

© 2020 Emad-Eldin A. A. Aly.

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

* Address correspondence to this author at Department of Statistics & Operations Research Faculty of Science, Kuwait University, Safat 13060, Kuwait;
Tel: +965 66655671; E-mail: eealy50@gmail.com


Abstract

Objectives:

To study the asymptotic theory of the randomly wieghted partial sum process of powers of k-spacings from the uniform distribution.

Methods:

Earlier results on the distribution of the uniform incremental randomly weighted sums.

Methods:

Based on theorems on weak and strong approximations of partial sum processes.

Results and conculsions:

Our main contribution is to prove the weak convergence of weighted sum of powers of uniform spacings.

Keywords: Uniform spacings, Weak convergence, Gaussian process, Incremental asymptotic convergence, Random Sample, k spacings.

1. INTRODUCTION

Let 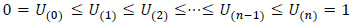be the order statistics of a random sample of size (n-1) from the U(0,1) distribution. Let k=1,2, ... be arbitrary but fixed and assume that n=mk. The U(0,1) k-spacings are defined as

(1)

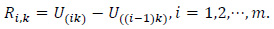
Let X1, X2,... be iidrv with E(Xi)=µ, Var(Xi)=ó2<∞ and common distribution function F(.). Assume that the Xi’s are independent of the Ui's. Define

(2)

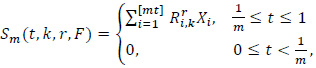
where [s] is the integer part of s and r>0 is fixed.

Looking at Sm (t,k,r,F) of (2) as a weighted partial sum of the X's, Van Assche [1] obtained the exact distribution of S2 (1, 1,1, F). Johnson and Kotz [2] studied some generalizations of Van Assche results. Soltani and Homei [3] considered the finite sample distribution of Sn (1,1,1, F). Soltani and Roozegar [4] considered the finite sample distribution of a case similar to Sm (1,k,1, F) in which the spacings (1) are not equally spaced. It is interesting to note that Sm (t,k,r, F) of (2) is also a randomly weighted partial sum of powers of k-spacings from the U(0,1) distribution.

Here, we will obtain the asymptotic distribution of the stochastic process

(3)

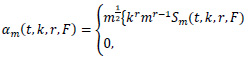
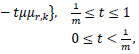
where

(4)

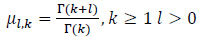
and Γ(.) is the gamma function.

The motivations and justifications of this work are given next. First, as noted by Johnson and Kotz [2], S2 (1,1,1, F) is a random mixture of distributions and as such it has numerous applications in Sociology and in Biology. Second, the asymptotic theory of Sm (t,k,r, F) is a generalization of important results of Kimball [5], Darling [6], LeCam [7], Sethuraman and Rao [8], Koziol [9], Aly [10] and Aly [11] for sums of powers of spacings from the U(0,1) distribution. Finally, we solve the open problem of proving the asymptotic normality of Sm (1,k,1, F) proposed by Soltani and Roozegar [4].

2. METHODS

2.1. The asymptotic distribution of αm (., k,r, F)

Let Y1,Y2,... be iidrv with the exponential distribution with mean 1 which are independent of the Xi's. By Proposition 13.15 of Breiman [12] we have for each n,

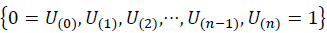
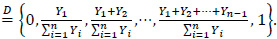
Hence, for each m,

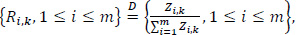
where for 1≤i≤m,

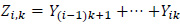
are iid Gamma (k,1) random variables. Hence, for each m

(5)

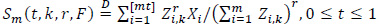
and

(6)

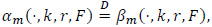
where

(7)

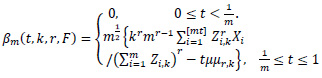
Let µl,k be as in (4). Note that

(8)

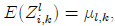
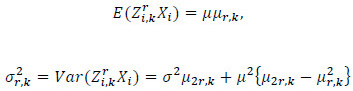
and

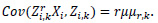
The following Theorem will be needed in the sequel.

Theorem A. There exists a probability space on which a two-dimensional Wiener process 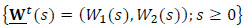is defined such that

(9)

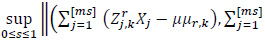
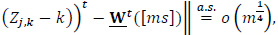
where E W (s)=0, and

(10)

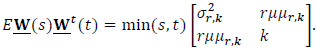
Theorem A follows from the results of Einmahl [13], Zaitsev [14] and Götze and Zaitsev [15].

The main result of this paper is the following Theorem.

Theorem 1. On some probability space, there exists a sequence of mean zero Gaussian processes Γm(t, k, r, F), 0≤t≤1 such that

(11)

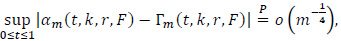
where 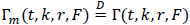for each m, and

(12)

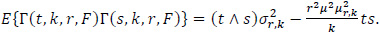
Theorem 1 follows from (6) and the following Theorem.

Theorem 2. On the probability space of Theorem A,

(13)

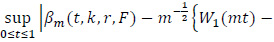
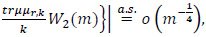
where W (.) is as in (9).

Proof of Theorem 2: We will only prove here the case when E(X)=µ≠0. The case when µ=0 is straightforward and can be looked at as a special case of the case µ≠0. Note that

(14)

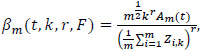
where

(15)

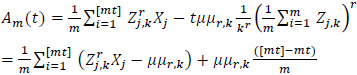
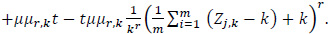
It is clear that, uniformly in t, 0≤t≤1,

(16)

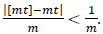
By (9), (15) and (16) we have, uniformly in t,0≤t≤1,

(17)

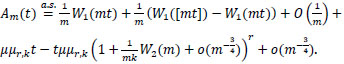
By Lemma 1.1.1 of Csörgö and Révész [17] we have, uniformly in t,0≤t≤1,

(18)

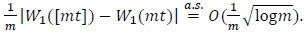
By (17) and (18) we have, uniformly in t,0≤t≤1,

(19)

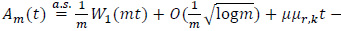
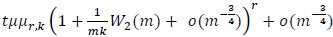
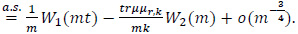
By the LIL

(20)

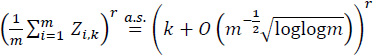
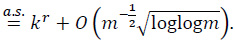
By (14), (19) and (20) we have, uniformly in t,0≤t≤1,

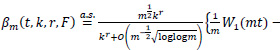
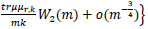
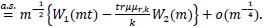
This proves (13).

Corollary 1. By (4), (8) and (12),

(21)

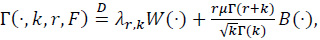
where

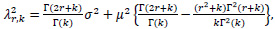
W(.) is a Wiener process, B(.) is a Brownian bridge and W(.) and B(.) are independent.

Corollary 2. By (11) and (21) we have, as m→∞,

(22)

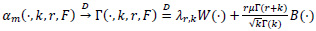
and, in particular,

(23)

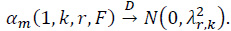
Some special cases of (22) and (23) are given . For r=1 and k≥1,

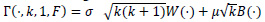
and

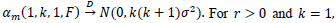
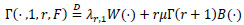
and

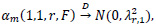
where

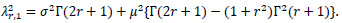
3. RESULTS

In this section, we will use the same notation of Section 1

3.1. The scaled sum case

Define

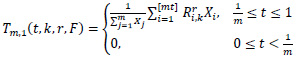
and

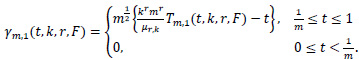
We can prove that

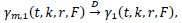
where

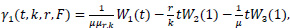
(W1(.),W2(.),W3(.))t is a mean zero Gaussian vector with covariance (t Λ s) ∑ 1‍ and

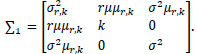
Let

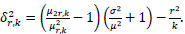
We can show that

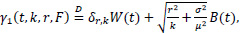
where W(.) is a Brownian Motion and B(.) is a Brownian bridge and W(.) and B(.) are independent. Consequently,

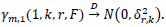
When r=1,k≥1

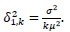
When r>0,k=1

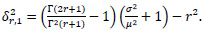
3.2. The Centered Sum Process

Let 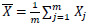and define

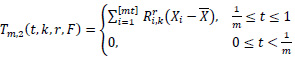
and

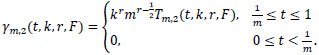
We can prove that

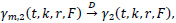
where

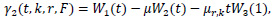
(W1(.), W2(.), W3(.))t is a mean zero Gaussian vector with covariance (t Λ s) ∑2 and

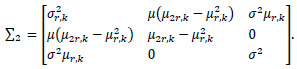
We can show that

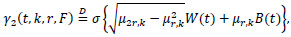
where W(.) is a Brownian Motion and B (.) is a Brownian bridge and W(.) and B(.) are independent. Consequently,

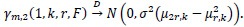
When r=1,k≥1

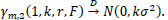
When r> 0,k=1

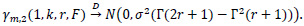
3.3. The Renewal Process

For simplicity, we will consider the case of r=1. Define

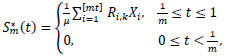
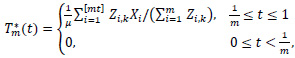
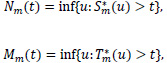
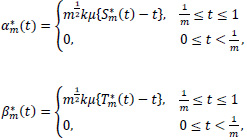
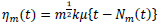
and

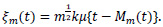
By (5), for each m

(24)

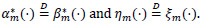
Note that (see (3))

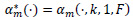
and hence, by Theorem 1

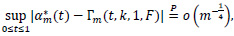
where Γm (., k, 1, F) is as in (11).

Theorem 3. On the probability space of Theorem A,

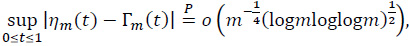
where

(25)

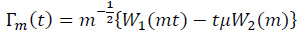
and W(.) is as in (9).

Theorem 3 follows directly from (24) and the following Theorem.

Theorem 4. On the probability space of Theorem A,

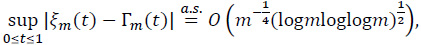
where Γm(t) is as in (25).

Proof: By (7),

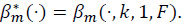
Note that

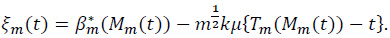
Hence

(26)

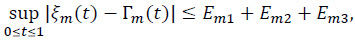
where

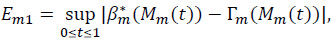
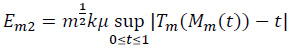
and

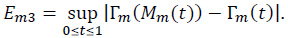
By Theorem 2 and the LIL for Wiener processes,

(27)

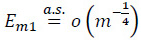
and

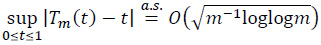
By a Lemma of Horváth [18]

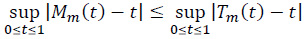
and hence

(28)

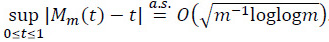
By the proof of Step 5 of Horváth [18] and Theorem 2 we can show that

(29)

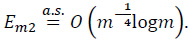
As to Em3,

(30)

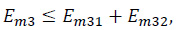
where

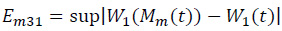
and

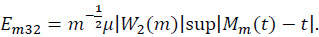
By (28) and Lemma 1.1.1 of Csörgö and Révész [17] we have, uniformly in t,0≤t≤1,

(31)

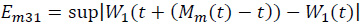
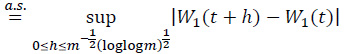
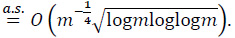
By (28) and the LIL for Wiener processes,

(32)

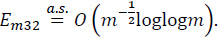
By (30)-(32),

(33)

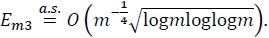
By (26)-(33) we obtain Theorem 4.

4. THE RANDOM VECTOR CASE

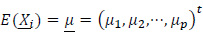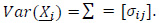Let X1, X2,... be iid random vectors with and Assume that the Ui's and the Ri,ks are same as in Section 1 and are independent of X1, X2,... Define

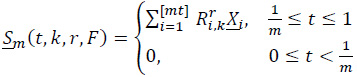
and

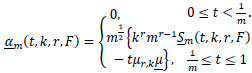
Theorem 5 is a generalization of Theorem 1.

Theorem 5. On some probability space, there exists a mean zero sequence of Gaussian processes 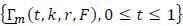such that

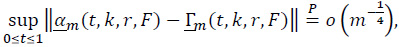
where, for each m,

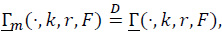
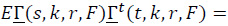
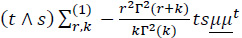
and

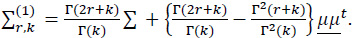
Corollary 1 *. By (11) and (21) we have, as m→∞,

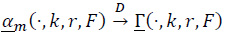
and, in particular,

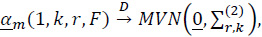
where

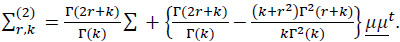
Particular cases of Corollary 1* are given next.

For r = 1 and k ≥ 1,

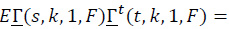
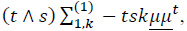
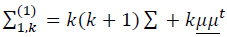
and

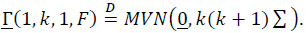
For r > 0 and k = 1,

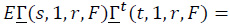
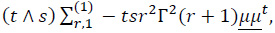
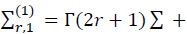
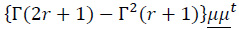
and

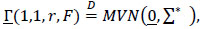
where

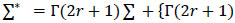
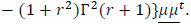
CONCLUSION

We proved the weak convergence of a stochastic process defined in terms of partial sums of randomly weighted powers of uniform spacings. The asymptotic results of several important generalizations and special cases are given.

CONSENT FOR PUBLICATION

Not applicable.

AVAILABILITY OF DATA AND MATERIALS

Not applicable.

FUNDING

None.

CONFLICT OF INTEREST

The author declare no conflict of interest, financial or otherwise.

ACKNOWLEDGEMENTS

Declared none.

REFERENCES

[1] Van Assche W. A random variable uniformly distributed between two independent random variables. Sankhya A 1987; 49(2): 207-11.
[2] Johnson NL, Kotz S. Randomly weighted averages: Some aspects and extensions. Am Stat 1990; 44(3): 245-9.
[3] Soltani AR, Homei H. Weighted averages with random proportions that are jointly uniformly distributed over the unit simplex. Stat Probab Lett 2009; 79(9): 1215-8.
[4] Soltani AR, Roozegar R. On distribution of randomly ordered uniform incremental weighted averages: Divided difference approach. Stat Probab Lett 2012; 82(5): 1012-20.
[5] Kimball HE. On the asymptotic distribution of the sum of powers of unit frequency differences. Ann Math Stat 1950; 21(2): 263-71.
[6] Darling DA. On a class of problems related to the random division of an interval. Ann Math Stat 1953; 24(2): 239-53.
[7] LeCam L. Un theoreme sur la division d’un intervalle par des points pris au hasard. Publ Inst Stat Univ Paris 1958; 7(3/4): 7-16.
[8] Sethuraman J, Rao JS. Weak convergence of empirical distribution functions of random variables subject to perturbations and scale factors. Ann Stat 1975; 3(2): 299-313.
[9] Koziol JA. A note on limiting distributions for spacings statistics. Z Wahrsch Verw Gebiete 1980; 51(1): 55-62.
[10] Aly E-EAA. Some limit theorems for uniform and exponential spacings Canad J Statist 1983; 11(1): 211-9.
[11] Aly E-EAA. Strong approximations of quadratic sums of uniform spacings. Can J Stat 1988; 16(2): 201-7.
[12] Breiman L. Probability 1968.
[13] Einmahl U. Extension of results of Komlós, Major and Tusnády to the multivariate case. J Mult Anal 1989; 28(1): 20-68.
[14] Zaitsev AYu. Multidimensional version of the results of Komlós, Major and Tusnády for vectors with finite exponential moments. ESAIM Probab Stat 1998; 2: 41-108.
[15] Götze F, Zaitsev AYu. Bounds for the rate of strong approximation in the multidimensional invariance principle. Theory Probab Appl 2008; 53(1): 100-23.
[16] Csörgö M, Horváth L. Weighted Approximations in Probability and Statistics 1993.
[17] Csörgö M, Revesz P. P, Strong Approximations in Probability and Statistics 1981.
[18] Horváth L. Strong approximation of renewal processes. Stochastic Process Appl 1984; 18(1): 127-38.