RESEARCH ARTICLE
Comparing Different Information Levels
Uwe Saint-Mont*
Article Information
Identifiers and Pagination:
Year: 2017Volume: 8
First Page: 7
Last Page: 18
Publisher Id: TOSPJ-8-7
DOI: 10.2174/1876527001708010007
Article History:
Received Date: 06/03/2017Revision Received Date: 19/04/2017
Acceptance Date: 27/04/2017
Electronic publication date: 19/07/2017
Collection year: 2017
open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Objective:
Given a sequence of random variables X = X1, X2, . . .suppose the aim is to maximize one’s return by picking a ‘favorable’ Xi. Obviously, the expected payoff crucially depends on the information at hand. An optimally informed person knows all the values Xi = xi and thus receives E(sup Xi).
Method:
We will compare this return to the expected payoffs of a number of gamblers having less information, in particular supi(EXi), the value of the sequence to a person who only knows the random variables’ expected values.
In general, there is a stochastic environment, (F.E. a class of random variables C), and several levels of information. Given some XϵC, an observer possessing information j obtains rj(X). We are going to study ‘information sets’ of the form.
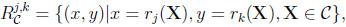 |
characterizing the advantage of k relative to j. Since such a set measures the additional payoff by virtue of increased information, its analysis yields a number of interesting results, in particular ‘prophet-type’ inequalities.




