RESEARCH ARTICLE
Skewness-Kurtosis Controlled Higher Order Equivalent Decisions
Wolf-Dieter Richter*
Article Information
Identifiers and Pagination:
Year: 2016Volume: 7
First Page: 1
Last Page: 9
Publisher Id: TOSPJ-7-1
DOI: 10.2174/1876527001607010001
Article History:
Received Date: 8/11/2015Revision Received Date: 9/12/2015
Acceptance Date: 10/12/2015
Electronic publication date: 20/04/2016
Collection year: 2016
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution-Non-Commercial 4.0 International Public License (CC BY-NC 4.0) (https://creativecommons.org/licenses/by-nc/4.0/legalcode), which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
Abstract
We define equivalence of asymptotic Gaussian expectation tests when error probabilities of first kind are approaching zero at the same restricted speed for both tests and if the same holds true for the error probabilities of second type which are measured at a moderate locally chosen alternative. To ensure such equivalence, the influence of skewness and kurtosis parameters is studied.
1. INTRODUCTION
Asymptotic relative efficiency of one test with respect to (w.r.t.) another is extensively studied in the literature. For an introduction and overview we refer to Nikitin [1]. Several notions of efficiency may be distinguished w.r.t. how the probabilities of first and second kind test errors behave in the case of increasing sample sizes. Roughly spoken, studies of Pitman type are dealing with situations where both kinds of probabilities of test errors stabilize asymptotically at some fixed positive levels while studies of different other types take into consideration that both error probabilities are tending to zero or that one of them stabilizes asymptotically at a positive value and the other one tends to zero. Moreover, one may take into account different speeds of convergence of the two error probabilities.
The present study deals with specific situations where probabilities of both error types are tending to zero not faster than at a certain moderate speed. Note that there are different notions of large and moderate deviations in the literature of probability theory and mathematical statistics. Zons of large deviations concerned here are often called to be of the so called Linnik type, and the speed at which error probabilities are tending to zero is controlled here by a so called Osipov condition.
Second type error probabilities of a test depend on the alternatives taken under consideration. While local asymptotic normality theory is in case of sample size n concerned with differences of parameters under the hypothesis and under the alternative being of the type
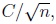 here we are dealing with such differences of the type
here we are dealing with such differences of the type
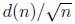 where
where
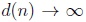 and
and
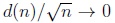 as
as
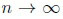 . Alternatives of the latter type will be called moderate local alternatives.
. Alternatives of the latter type will be called moderate local alternatives.
Numerous statistical and probabilistic results have been derived for such situations, see Inglot and Ledwina [2, 3], Kallenberg [4, 5], Kallenberg and Ledwina [6], Ledwina, Inglot and Kallenberg [7], Richter [8-10] and Wood [11].
The notion of probabilities of moderate deviations partly used in those papers should be distinguished from that used for deviations in logarithmic zones, e.g., in Amosova [12] and Richter [8, 13, 14] for the one and multi-dimensional case, respectively.
Recent extensions of related considerations to martingale sample schemes are to be found in Fan, Grama and Liu [15].
The paper is organized as follows. Section 2.1 provides an introduction to skewness-kurtosis adjustments of the classical asymptotic Gauss test following Richter [10], and a comparison to the well known Cornish-Fisher expansion. The equivalence of tests in the sense of Pitman is discussed in Section 2.2. The main result of this paper concerning skewness-kurtosis higher order equivalent decisions between a hypothesis and a moderate-local alternative is derived then in Section 3.
2. PRELIMINARIES
2.1. Skewness-kurtosis Adjusted Asymptotic Gauss Test
Let X1, ..., Xn be independent and identically as X distributed random variables with the common distribution law from a shift family of distributions, Pµ = P (· - µ), where the expectation equals µ, µ
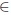 R, and the variance is σ2. Assume we are interested in deciding between a producer’s hypothesis and a customer’s apprehension,
R, and the variance is σ2. Assume we are interested in deciding between a producer’s hypothesis and a customer’s apprehension,
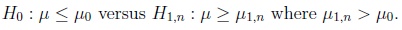 |
(1) |
The test partners are aware of the general circumstance that the values of the power function of a test are only larger than a reasonable bound if the argument of the function is chosen sufficiently far from those arguments representing the null hypothesis. They agree therefore to use a test reflecting this situation from the very beginning. The size of the gap between µ 0 and µ1,n depends on what the customer may be willing to tolerate in a given practical situation, both w.r.t. the absolute value of µ1,n-µ0 and w.r.t. the costs, expressed through the sample size n.
It is well known that the statistic
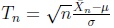 where
where
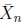 stands for the sample mean is asymptotically for
stands for the sample mean is asymptotically for
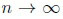 standard normally distributed, Tn ~ AN (0, 1). Hence,
standard normally distributed, Tn ~ AN (0, 1). Hence,
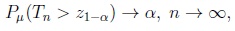 |
and under the n-1/2-local non-true parameter assumption,
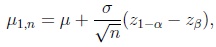 |
i.e. if one assumes that a sample is drawn with a shift of location or with an error in the variable, then
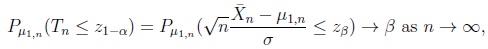 |
where zq denotes the quantile of order q of the standard Gaussian distribution, and α, β are from the interval (0, 1/2). Thus, the first and second type error probabilities of the decision rule
 of the asymptotic Gauss test satisfy the asymptotic relations
of the asymptotic Gauss test satisfy the asymptotic relations
 |
Refinements of
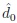 and of these two asymptotic relations where α = α(n) → 0 and β = β(n) → 0 as n → ∞ were proved in Richter [10] under suitable additional assumptions.
and of these two asymptotic relations where α = α(n) → 0 and β = β(n) → 0 as n → ∞ were proved in Richter [10] under suitable additional assumptions.
It is often said that a random variable X satisfies the Linnik condition of order γ, 0 < γ < 1/2, if
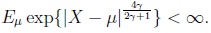 |
(2) |
This condition and far reaching consequences from it for probabilities of large deviations have been studied in Ibragimov and Linnik [16] (for a more general condition see Linnik [17]) and a subsequent series of papers by many authors of whom we refer here to Nagajev [18] and Richter [19] where condition (2) was fundamentally generalized in two steps.
Two sequences of probabilities, (α(n)) n=1,2,... and (β(n)) n=1,2,..., are said to satisfy an Osipov-type condition of order γ if
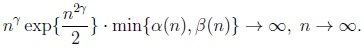 |
(3) |
This condition was originally introduced in Osipov [20] for considering large deviations of multivariate random vectors. Several consequences following from (3) for probabilities of moderate and large deviations in finite dimensions have been studied, e.g., in Richter [8, 13, 21].
Condition (3) means that neither α(n) nor β(n) tends to zero as fast as or even faster than n-γ exp{-n2γ /2}, i.e.
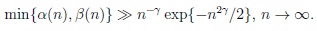 |
On using Gaussian quantiles this condition may be written
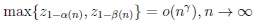 |
where o(.) stands for the small Landau symbol. Note that large Gaussian quantiles satisfy the asymptotic representation
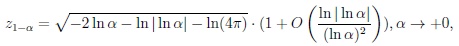 |
see Ittrich, Krause and Richter [22] and Richter [10].
Skewness-kurtosis adjustments of the asymptotic Gauss test make use of the following quantities. The first and second kind (or order) adjusted asymptotic Gaussian quantiles are defined by
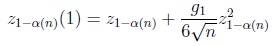 |
(4) |
and
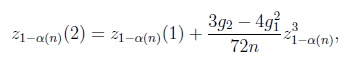 |
(5) |
respectively. Here,
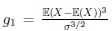 and
and
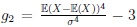 are skewness and kurtosis of X, respectively. Similarly, the first and second kind modified non-true moderate local parameter choices are
are skewness and kurtosis of X, respectively. Similarly, the first and second kind modified non-true moderate local parameter choices are
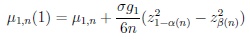 |
and
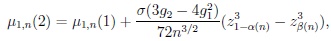 |
respectively. The first and second kind adjusted decision rules
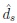 of the one-sided asymptotic Gauss test determine to reject H 0 if Tn,0 > z1-α(n)(s) for s = 1 or s = 2 respectively, where
of the one-sided asymptotic Gauss test determine to reject H 0 if Tn,0 > z1-α(n)(s) for s = 1 or s = 2 respectively, where
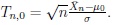
Let us recall that if two functions f, g satisfy the asymptotic
relation
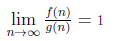
then this asymptotic equivalence will be written f (n) ~ g (n), n → ∞.
It was proved in Richter [10] that if the conditions (2) and (3) are satisfied for a certain γ,
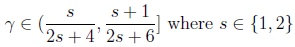 |
(6) |
then the error probabilities of the adjusted decisions satisfy
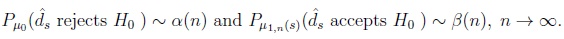 |
(7) |
These results have been equivalently reformulated in Richter [10] with the help of the first and second kind adjusted asymptotically Gaussian test statistics
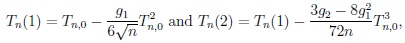 |
respectively. The hypothesis H 0 will be rejected according to decision rule
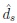 if Tn(s) > z1-α(n), and the first and second kind error probabilities of this decision still behave as in (7).
if Tn(s) > z1-α(n), and the first and second kind error probabilities of this decision still behave as in (7).
Similar consequences for testing H 0 : µ > µ 0 or H 0 : µ ≠ µ 0, as well as for constructing confidence intervals, are omitted here.
The material of this section surveys the condensed content of the basic ’testing-part’ of what was presented by the author at the Conference of European Statistics Stakeholders, Rome 2014, (see Abstracts of Communication, p. 90 and Richter [10]) where, however, the equivalent ’language’ of confidence estimation is used. The advanced ’testing-part’ of this talk is presented in Section 3 of the present paper.
Remark 2.1. From a formal point of view, the first and second kind adjusted asymptotic Gaussian quantiles defined in (4) and (5), respectively, have the same analytical structure as the coefficients of a Cornish-Fisher quantile-expansion (CFE), see Fisher and Cornish [23] and Bolschev and Smirnov [24]. However, CFE is valid for fixed or stabilizing values of α while the relations in (4) and (5) apply to the case α ( n) → 0 as n → ∞. Taking this into account, the large deviation results in their form presented here through a new light onto the CFE. Note that the CFE itself is based upon an Edgeworth type expansion of a corresponding cumulative distribution function. Theoretical and numerical comparisons of normal and large deviation approximations for tail probabilities were presented in Field and Ronchetti [25], Fu,Len and Peng [26], Ittrich, Krause and Richter [22] and Jensen [27].
2.2. Pitman Equivalent Tests
In production process control, assume two methods are available for measuring the dimension µ of a workpiece which is serially made on a machine. In general, either methods work at different levels of costs and precision, the latter being expressed in terms of variances of measurements, σ12 and σ22. One may be interested then in knowing for which sample size n2 = n2(n1) the second method works as good as the first one works for sample size n1. For comparing the two methods of process control being based upon the two methods of measuring a workpiece one may compare both first and second kind error probabilities when dealing with problem (1) where we are given now the i.i.d. samples
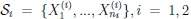 satisfying
satisfying
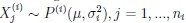 with
with
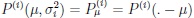 for any probability distribution law from a family having shift parameter equal to expectation µ, and variance σi2, i = 1, 2. Throughout what follows in the present paper all statistics built on using the random variables X(i)j , as well as quantiles of their distribution functions, will be indicated by an upper subscript, and their higher order moments and semi-invariants as well as corresponding sample sizes will be indicated by the (possibly second) lower index i.
for any probability distribution law from a family having shift parameter equal to expectation µ, and variance σi2, i = 1, 2. Throughout what follows in the present paper all statistics built on using the random variables X(i)j , as well as quantiles of their distribution functions, will be indicated by an upper subscript, and their higher order moments and semi-invariants as well as corresponding sample sizes will be indicated by the (possibly second) lower index i.
In this sense,
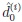 denotes the decision function based upon the asymptotically Gaussian statistic Tni(i) evaluated for sample
denotes the decision function based upon the asymptotically Gaussian statistic Tni(i) evaluated for sample
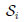 of size ni, i = 1, 2.
of size ni, i = 1, 2.
We recall that Pitman’s strategy of defining equivalence of two tests is one of several such strategies which are commonly formulated for rather general tests, see, e.g., in Nikitin [1]. We restrict our consideration here, however, to pairs of tests based upon the statistics Tni(i) being the suitably centered and normalized means of the i.i.d.-samples
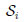 , i = 1, 2.
, i = 1, 2.
Two such test sequences based upon samples of sizes n1, n2 where n2 = n2(n1) → ∞ as n1 → ∞ and decisions
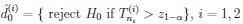 |
are called asymptotically (α, β)-Pitman equivalent for deciding the problem (1) with
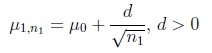 |
(8) |
if
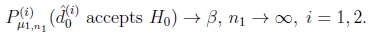 |
(9) |
We shall refer to this as first order equivalence of decisions
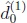 and
and
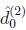 . Note that here
. Note that here
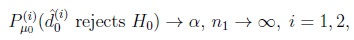 |
(10) |
and α and β are assumed to belong to the interval (0, 1/2). It turns out that asymptotic (α, β)-Pitman equivalence holds if
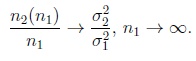 |
(11) |
3. HIGHER ORDER EQUIVALENCES
Let us assume throughout this section that as before n2 = n2(n1) → ∞ as n1 → ∞ but, differently from Section 2, first and second type error probabilities are tending now to zero, and
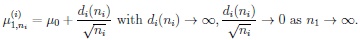 |
The latter assumption means that, for n1 → ∞, the sequences of alternative moderate local non-true parameters are tending not as fast to µ0 as before.
Let the first and second order adjusted decision functions
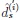 be defined as to decide between
be defined as to decide between
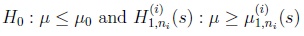 |
(12) |
by rejecting H0 if
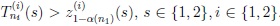 For a discussion of the meaning and the size of the gap between µ0 and
For a discussion of the meaning and the size of the gap between µ0 and
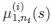 , we refer to what was said just following (1). We recall that the moderate local alternatives
, we refer to what was said just following (1). We recall that the moderate local alternatives
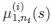 allow according to Section 2 the representation
allow according to Section 2 the representation
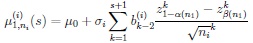 |
where
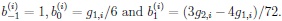 Note that the sizes of the first and second kind error probabilities α(.) and β(.), respectively, are chosen independently of i, i
Note that the sizes of the first and second kind error probabilities α(.) and β(.), respectively, are chosen independently of i, i
 {1, 2}.
{1, 2}.
Definition 3.1. The decisions
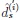 , i = 1, 2 are said to be asymptotically moderate locally equivalent of order s + 1, s
, i = 1, 2 are said to be asymptotically moderate locally equivalent of order s + 1, s
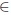 {1, 2} for deciding the problem (12) with
{1, 2} for deciding the problem (12) with
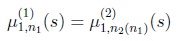 |
(13) |
if, for n2(n1) → ∞ as n1 → ∞,
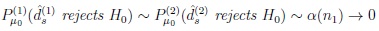 |
and
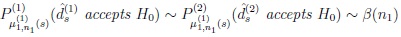 |
where α(n1), β(n1) satisfy the Osipov type condition (3) with γ chosen according to (6).
Theorem 3.1. Let X1(1) and X1(2) satisfy the Linnik condition (2) for one and the same γ = γ(s) fulfilling (6). Moreover, let α(n1), β(n1) satisfy the Osipov condition (3) for the same γ = γ(s), and assume that
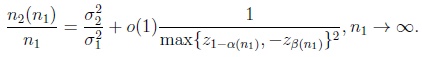 |
(14) |
If in the case s = 1 skewness g1,1 and g1,2 of X(1) and X(2), respectively, satisfy
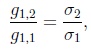 |
(15) |
and if in the case s= 2 additionally the corresponding kurtosis values satisfy
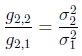 |
(16) |
then
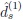 and
and
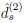 are equivalent of order s + 1, s
are equivalent of order s + 1, s
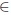 {1, 2}, respectively.
{1, 2}, respectively.
Proof. The proof of the first property of Definition 3.1 follows directly from the results in Richter [10], see Section 2.1. We recall that if condition (3) is satisfied then x = z1-α(n) = o(nγ), n → ∞ for γ
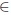 (1/6 , 3/10], and if (2) is satisfied then, according to Nagajev [18] and Petrov [28],
(1/6 , 3/10], and if (2) is satisfied then, according to Nagajev [18] and Petrov [28],
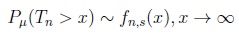 |
(17) |
where
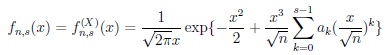 |
and s is an integer satisfying (6), i.e. s = 1 if γ
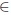 (1/6, 1/4] and s = 2 if γ
(1/6, 1/4] and s = 2 if γ
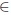 (1/4, 3/10].
(1/4, 3/10].
Here, the constants
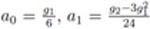 depend on skewness g1 and kurtosis g2 of X.
depend on skewness g1 and kurtosis g2 of X.
Thus, according to the construction of the skewness-kurtosis adjusted quantiles
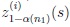 and moderate local alternatives
and moderate local alternatives
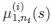 , i
, i
 {1, 2}, s
{1, 2}, s
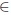 {1, 2},
{1, 2},
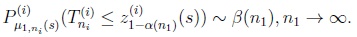 |
(18) |
Hence, for proving the second property of Definition 3.1 it remains to show that one can replace
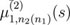 with
with
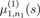 in (18) if there holds i = 2.
in (18) if there holds i = 2.
As a consequence of (17), and in accordance with the proof of Theorems 1 and 2 in Richter [10],
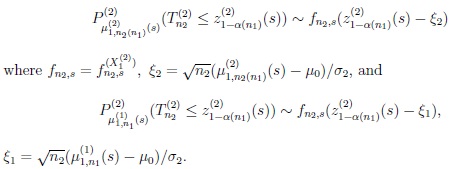 |
It remains therefore to show that,
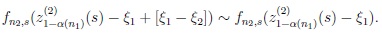 |
Equivalently, we prove that,
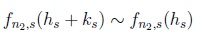 |
(19) |
with
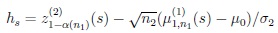 |
and
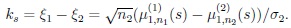 |
According to Lemma 3.1 below, for proving (19) it is sufficient to prove that ks = o(hs-1). Note that,
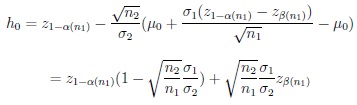 |
and
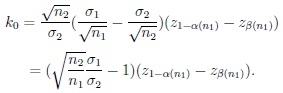 |
By (14),
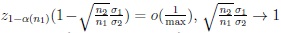 and zβ(n1) → -∞ as n1 → ∞ where max = max {z1 - α(n1), -zβ(n1)}. It follows, symbolically, that,
and zβ(n1) → -∞ as n1 → ∞ where max = max {z1 - α(n1), -zβ(n1)}. It follows, symbolically, that,
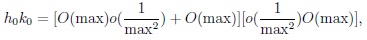 |
thus h0 k0 = o(1) as n1 → ∞. Moreover,
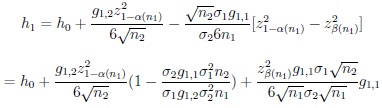 |
and
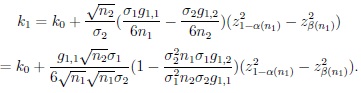 |
If s = 1 then because of (15) and (14),
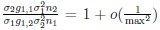 and
and
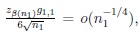 thus h1k1 = o(1). Similarly, on using (16) and (14), in the case s = 2, h2k2 = o(1).
thus h1k1 = o(1). Similarly, on using (16) and (14), in the case s = 2, h2k2 = o(1).
Lemma 3.1. If
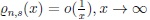 then
then
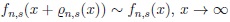 Proof. Let
Proof. Let
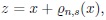 then
then
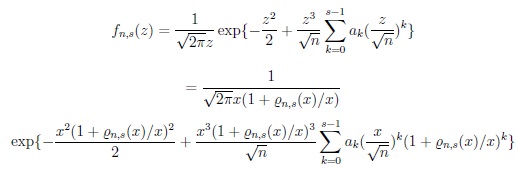 |
~ fn,s(x ) if (i)
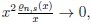 , (ii)
, (ii)
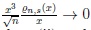 and (iii)
and (iii)
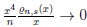 . Note that assumption (i) is a stronger one than (ii) and (iii), and that it is fulfilled under the assumptions of Lemma 3.1.
. Note that assumption (i) is a stronger one than (ii) and (iii), and that it is fulfilled under the assumptions of Lemma 3.1.
CONFLICT OF INTEREST
The author confirms that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
The author is grateful to the Reviewers for carefully reading the paper and giving valuable hints leading to an improvement of the paper.




