RESEARCH ARTICLE
A More Suitable Definition of Quadratic Surds
Orchidea Maria Lecian1, *
Article Information
Identifiers and Pagination:
Year: 2020Volume: 10
First Page: 8
Last Page: 20
Publisher Id: TOSPJ-10-8
DOI: 10.2174/2666148902010010008
Article History:
Received Date: 21/12/2019Revision Received Date: 02/05/2020
Acceptance Date: 20/08/2020
Electronic publication date: 23/10/2020
Collection year: 2020
open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Background:
The properties of the group PGL(2,C) on the Upper Poincar´e Half Plane have been analyzed.
Objective:
In particular, the classification of points and geodesics has been achieved by considering the solution to the free Hamiltonian associated problem.
Methods:
The free Hamiltonian associated problem implies to discard the symmetry sl(2,Z) for the definition of reduced geodesics. By means of the new definition and classification of reduced geodesics, new construction for tori, punctured tori, and the tessellation of the Upper Poincar´e Half Plane is found.
Results:
A definition of quadratic surds is proposed, for which the folding group corresponds to the tiling group, (also) for Hamiltonian systems on the Hyperbolic Plane (also realized as the Upper Poincar´e Half Plane (UPHP)).
Conclusion:
The initial conditions determine the result of the folding of the trajectories as tiling punctured tori and for tori.
1. INTRODUCTION
The analysis of the solutions of Hamiltonian systems on the Upper Poincar´e Half Plane (UPHP) allows to outline the differences between the possible tessellation groups of the system and the folding groups for · chaotic systems. The symmetry groups which leave the solution of the Hamiltonian system unchanged allow one to define the folding group(s) for the problem, the (expression(s) defining the) shape(s) [1] of the potential being considered, as studied by G.C Layek [2]. The correspondences with the tiling group of the Poincar´e Plane associated with the same problem can be investigated.
This approach follows the hints by C. Series [3] about open issues (emerging after the work by C. Series [4] and [5]) in tessellating the Hyperbolic Plane.
Considering (the solutions of) a Hamiltonian system allows one to investigate the properties of the action of the PGL(2,C) group on the Poincar´e Plane and needs the construction indicated by A. Terras [2] of the proper congruence subgroups designated by N.I. Koblitz [6]. The correspondences and the differences between the two approaches are directly outlined.
A definition for quadratic surds in Hamiltonian problems is also proposed for the Gauss-Kuzmin Theorem (where the latter is summarized, i.e., by S.J. Miller and R. Takloo-Bighash [7]) which is to be applied [8, 9].
The Hamiltonian approach allows one to consider geodesics, and, on them, the solutions to the equations of motion as segments of geodesics, where the (set of initial condition(s) chose an orientation for the oriented endpoints. The problem of rational geodesics is described according to its dynamical properties.
As outlined by R. Adler and L. Flatto [10], the geometrical measure is needed to be invariant under the (transformations associated with) Hamiltonian flow.
Hamiltonian problems on Hecke triangles have been investigated by D. Mayer and F. Stroembergin [11]. In particular, the group PSL(2,Z) is analyzed as a conjugate to a congruence subgroup of the modular group. The interest in the role of arithmetical groups and semi-arithmetical groups is raised. Natural extensions of the symbolic dynamics are proposed.
The need for the structure PSL(2,Z) has been recalled for the Hamiltonian formulation of chaotic systems in closed domains (generalized triangles) on surfaces of constant negative curvature by D. Fried [12].
Within the proposed approach, the guidelines of R. Adler and L. Flatto [10] are followed to address the existence and the description of periodic orbits and of rational orbits for the (generalized) triangles, which derive from the systems investigated by C. Series [4], and [5]. The analysis of the associated Hamiltonian systems is implied by the necessity to describe geodesics (on which orbits lay) as originating from specific initial conditions or specific boundary conditions, and, in the first case, also after a specific continuous (set of) transformation(s). The folding of particular geodesics is consistent with the construction of ’punctured’ tori and of tori.
Instead of studying the action of arithmetical groups and of semi-arithmetical groups on geodesics in generalized triangles (for which such triangles stay invariant because of the invariance of the geometrical measure), to bring together the analyses of D. Mayer and F. Stroembergin [11] and D. Fried [12], here the Hamiltonian systems for generalized triangles (and, in particular, also Hecke triangles) are proved to stay invariant as described by suitable congruence subgroups of PGL(2,C) rather than of PGL(2,Z), because, in this case, also the invariance under generic translations and dilations is assured.
In particular, a generic dilation is an inversion of a geodesics with respect to a geodesic circumference, which is not achieved by PGL(2,Z); also generic translations are not described by this group. Furthermore, generic triangles are not described as congruence subgroups of PGL(2,Z).
By means of the PGL(2,C) group and its congruence subgroups, it is possible to determine the tessellation of the Poincar´e Upper Half Plane needed to describe generic triangles and different cases of tori as the non-limiting process and/or the limiting process of the tessellation with respect to the tiling group individuated by the folding implied by the Hamiltonian flow. This way, the biggest group, which leaves invariant the Hamiltonian flow and the related geometrical measure is PGL(2,C).
As a result, the transformations required by the definition of congruence subgroups are assumed to be continuous by means of the analysis of the corresponding Hamiltonian problem. The tiling group for the Hamiltonian systems and the folding group for their solutions coincide and are constructed by a (composition of) continuous transformation(s) for each suitable congruence subgroup (i.e. according to the transformation(s) needed to evolve the initial conditions). As particular cases, punctured tori and tori are constructed by the tiling implied by the folding of particular orbits.
In the following, the dynamical system corresponding to a free particle on the desymmetrized domain of PGL(2,C) will be described. Reduced quadratic surds are classified for the values acquired by the endpoints of the geodesics oriented according to the solutions of the equations of motion. The corresponding set of allowed initial values defines rational trajectories for the Hamiltonian system among all the possible rational geodesics lying within the geometrical domain. The folding group for the dynamical system is demonstrated to coincide with the tiling group of the group domain. Particular trajectories (close to rational ones) are demonstrated to originate, by their folding, different kinds of tori, for which rational geodesics are defined and classified as well.
In particular, in the study by C. Series [4], the ’free group’ F on a torus on the Poincar´e Plane is analyzed to find out its action on cutting geodesics; in the present paper, in the following, such geodesics will further be classified as ’reduced surds’ according to the capability of the (smaller) group compatible with the associated Hamiltonian problem, and the possibility to apply the Gauss-Kuzmin theorem rather than the properties of Markoff chains used by C. Series [4], because of the properties of the congruence subgroups of F.
In the present work, the consideration of trajectories of the hyperbolic Poincar´e plane as solutions for a Hamiltonian system allows one to classify the initial conditions for the construction of tori and of punctured tori.
The quantum-mechanical-systems description associated is described by the author [13], also for the graded algebras of Hecke Groups and those for Winberg groups.
The aim of this analysis is to establish a more general definition for reduced geodesics (quadratic surds) for the group PGL(2,C) in hyperbolic geometry, on the Upper Poincar´e half plane; within this framework, the symmetry SL(2,Z) cannot be implemented. The geodesics solutions of the free Hamiltonian problem for the group PGL(2,C) are classified, and the parametrization for the reduced geodesics is found. Among these geodesics, periodic geodesics are parameterized, and the corresponding expressions in terms of finite reduced continued fractions are rewritten. By means of the definition of reduced geodesics, several new constructions of tori and of punctured tori for the group PGL(2,C) are achieved. The definitions provided are also employed for definitions of the tessellations of the Upper Poincar´e Half plane achieved by means of the considered group PGL(2,C), and compared with those obtained by means of other groups.
The paper is organized as follows.
In Section II, examples of classifications of points, geodesics, and their continued-fractions expressions for several for several groups on the Upper Poincar´e Half Plane are revised.
In Section III, generalized triangles are defined sectiona1 for the smallest domain.
In Section IV, a theorem for surds is stated. The Hamiltonian problem associated with a symmetry group is investigated. For the smallest domain, the group needed is PGL(2,C). For the equations of motion of Hamiltonian systems to be continuous, the symmetry SL(2,Z) has to be discarded (except for specific cases).
A definition of quadratic surds is given, which contains all the elements needed for the description of the tessellations following from the folding groups for the solutions and for the corresponding tiling group for the Poincar´e Plane. In Section V, rational geodesics admitted as a solution for the Hamiltonian system to the free Hamiltonian problems are classified.
In Section VI, tori are described as resulting from some limiting process in the tessellation of the Poincar´e Plane according to the folding of particular solutions, for which the limiting process is achieved by irrational orbits. In Section VII, ’punctured’ tori are defined according to similar tesselation techniques, which can be compared to the analysis proposed by C. Series [3-5].
In Section VIII, different tiling groups for the Poincar´e Plane have been illustrated to be non-efficient for the folding of the solutions of the Hamiltonian systems described in their domain.
Generalizations and further applications are discussed, and concluding remarks are also mentioned , IX follows.
2. SEVERAL DEFINITIONS OF CONTINUED FRACTIONS AND REDUCED CONTINUED FRACTIONS
The study of the properties of continued fractions corresponding to the hyperbolic geometry of the surfaces for Hecke groups has widely been investigated.
Some of the aspects of the congruence subgroup Γ0(m) of the linear-fractional transformations group have been studied by A.O.L. Atkin and J. Lehner [14]. All discontinuous groups on the hyperbolic plane have a connected fundamental domain, whose compactification points are cusps points, which can be rational points on the real axes, or points at infinity. Given a subgroup Γ with a cusp point, there exists a Hermitian operator wrt the scalar product, and there exists a basis for the Fourier decomposition of each complex-valued function on it, i.e. which are the eigenfunction of the translation operator and for any transformation Wq (where Wq is defined as (qβ,1;mγ,q) with (q2β − mγ = q)). The normalizer of Γ0 in GL+(2,Z) contains any product of Wq. The annihilator operator is well-defined. The vector space < Γ0(m),k >0 has a basis which is a direct sum of classes; every form in the same class admits the same eigenvalues of the operator Tp, for all primes p such that (p,m = 1). An alternative basis consists of forms that are eigenforms of all the Wq for q | m.
Lehner continued fractions Lcf(x), as characterized by J. Lehner [15], and K. Dajani and C. Kraaikamp [16], are
defined as
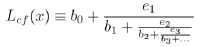 |
(1) |
for any irrational number x ϵ (1,2) and there exists the map LL(x) s.t.
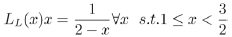 |
(2) |
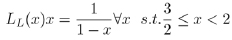 |
(3) |
The Lehner map and the Gauss-Kuzmin map are therefore inequivalent.
Chains of discontinuous fractions and discontinuous groups have been classified by D. Rosen (Rosen fractions), [17].
Given the group structure
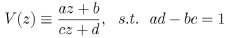 |
(4) |
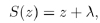 |
(5) |
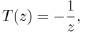 |
(6) |
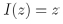 |
(7) |
with λ fixed real number and ad − bc real coefficients, the features of the corresponding Fuchsian group Γ(λ) can be analyzed, and, in particular, the features of the boundaries of the domain as far as the existence of continuous trajectories and cusp points are concerned by means of the Lehner fractions Eq. (1).
For a group Γ(λ), infinite continued fractions are expanded as
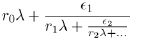 |
(8) |
with ǫ = ±1, ri integer rational, r ϵ N+, i ≥ 1, λ > 0 fixed.
A finite continued fraction is expressed by a finite number of components; as an example, the point is decomposed as a finite continued fraction
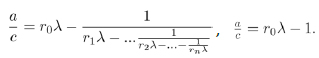 |
(9) |
of which the simplest example is 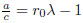 .
.
A point is a parabolic point if it is expressed by a finite continued fraction. The point 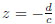 is a parabolic point. For λ = 2cos(π/q), q ≥ 4, or λ ≥ 2, when a real number α can be expressed by a reduced continued fraction (it corresponds to an α-Rosen continued fraction).
is a parabolic point. For λ = 2cos(π/q), q ≥ 4, or λ ≥ 2, when a real number α can be expressed by a reduced continued fraction (it corresponds to an α-Rosen continued fraction).
Rosen continued fractions can be used to study some particular features of Hecke groups. As an example of a particular group structure, studied by D. Rosen and T.A. Schmidt [18], given Gq a Hecke group of the first class
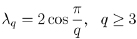 |
(10) |
with q ϵ Z, λ-periodic continued fractions determined by G, which correspond to periodic closed geodesics, are analyzed.
Given 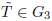
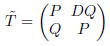 |
√D is periodic iff P2 − DQ2 = 1.
For q > 3, periodic continued functions are defined if there exists a solution to the Pell equation with DQ/P and P/Q consecutive convergents.
For Q(λq), a cusp point P/Q is defined by the continued fraction given the convergent Pn/Qn such that P/Q ≡ Pn/Qn
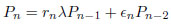 |
(11) |
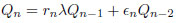 |
(12) |
which satisfies the determinant relation
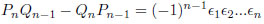 |
(13) |
Periodic √D/C geodesics, α(√D/C), with D square-free up to the unit, are defined as:
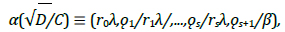 |
(14) |
, with 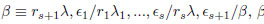 being, therefore, called the cyclic part.
being, therefore, called the cyclic part.
As investigated by T.A. Schmidt and M. Sheingorn [19], as far as the lengths of the spectra for Hecke triangular groups are concerned, given a Hecke group Gq on the upper Poincar´e half-plane H, the length of closed geodesics on GH is calculated after the Gq-equivalence for quadratic binary forms over Z[λq]. The discriminants for the reduced quadratic forms are listed explicitly.
T.A. Schmidt has investigated λ-Rosen continued spectrum with particular emphasis on the number-theoretical
aspects of the Markovv theory [20]: invariant measures for transformations of Hecke groups have been defined by means of the definition of the Rosen continued fractions.
In the case λq = λ4 = √2, in the interval 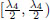 , the extended transformation M → M is defined
, the extended transformation M → M is defined
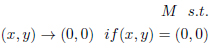 |
(15) |
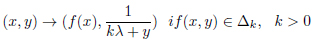 |
(16) |
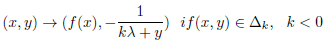 |
(17) |
where 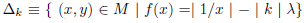 . The invariant measure for the transformation M, dM(x,y), is
. The invariant measure for the transformation M, dM(x,y), is 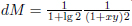 .
.
For Hecke triangles surfaces, as pointed out by T.A. Schmidt and M. Sheingorn [21], the equivalence of simple closed geodesics on GH and Γ/′ H does not hold for q > 7, where Γq′ is the commutator subgroup of Gq.
3. A DEFINITION FOR HYPERBOLIC TRIANGLES
The smallest domain considerable on the Poincar´e plane is the desymmetrized domain of the modular domain, such that
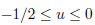 |
(18) |
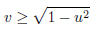 |
(19) |
on which the reflections group
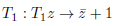 |
(20) |
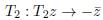 |
(21) |
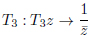 |
(22) |
defines the reflections of the geodesics on the sides of the domain as PGL(2,C).
Remark 1. The reflections with respect to geodesic (degenerate circumference(s)) (20), (21) lines and geodesics (non-degenerate circumferences (22)) are particular cases.
The associated dynamical problem is that solving the Hamiltonian of a free point particle moving inside the domain; the analysis of the solution of the equations of motion shows the motion is chaotic.
The metric-transitivity of transformations on generalized hyperbolic triangles, as indicated by G.A. Hedlund [22], for the more general case of closed surfaces of constant negative curvature, will be discussed at the end of the next Section.
4. A THEOREM FOR SURDS
It is useful to consider a definition of quadratic surds for Hamiltonian problems where the equation(s) of motion are continuous, for which the folding group and the tiling group coincide.
For future purposes, the quantity ∆x is defined as the maximum range of the real variable acquired by the potential shape. For the system (19), this interval is ∆x: −1/2 < x < 0.
The solution of the equations of motion z′ consists of a composition of the operators (21) acting on a geodesics z, and is represented, as hinted from E.B. Bogomolny, B. Georgeot, M.-J. Giannoni, C. Schmit [23], as
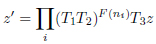 |
(23) |
with F(ni) ϵ N an opportune number, defining the number of iterations of the composed operator (resulting as a translation).
Periodic geodesics are particular solutions that leave (24) invariant, i.e. for z′ ≡ z. These solutions are classified as reduced quadratic surds. It is now possible to define them as in the following
Theorem 2. Reduced quadratic surds for the desymmetrized modular domain are those with oriented endpoints −2 ≤ x′ ≤ −1, x > 1.
Any different definition of x′, i.e. any continuous transformation of the interval [0,1], does not modify the pertinent properties of this interval, i.e. the distribution of numbers within this interval, according to the Gauss-Kuzmin Theorem as recalled by S.J. Miller and R. Takloo-Bighash [7].
Definition 3. The reduced surds for the free-particle Hamiltonian on a desymmetrized domain of PGL(2,C) are those with oriented endpoints −2 ≤ x′ ≤ −1, x > 1.
A definition for reduced quadratic surds corresponding to the oriented endpoints of (the geodesics defining) periodic trajectories of this dynamical system is derived from ancient definitions given, for more general cases for surds and particular cases of quadratic surds, by G.H. Hardy and F. Aicardi [8, 9], resp.
Remark 4. Because of the reflection (23), a definition of ’reduction’ is also needed for irrational (non-periodic) geodesics, because of the Gauss-Kuzmin Theorem.
According to these theorems, the initial conditions for trajectories define geodesics.
Particularly, rational geodesics enjoy the same classification as far as initial conditions for dynamical systems are concerned, even though they originate rational trajectories.
Specifically, such a definition allows one to extract items of information from the continued-fraction expansion of a number (i.e. from the fractional part of the value of the positively-oriented endpoint) after the reflection (23) has acted on z in (24) and allows one to apply the Gauss-Kuzmin theorem consistently, i.e. on the (wrt to initial conditions)-same digit of the continued fraction.
After the definition of initial conditions is achieved, the properties of the dynamical system are described uniquely by the symmetry group defined on the potential.
Corollary 5. The following statements are equivalent.
The action of the operators (21) on (19) tiles the Poincar´e Plane uniformly, i.e. with tiles of equal (with respect to the geometrical measure dudv/v2) area.
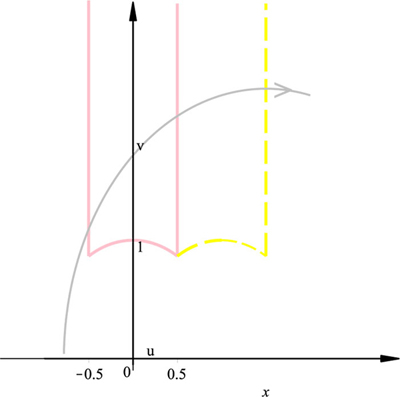
The tiling group for this domain corresponds to the folding group for the solutions of the equations of motion. The folding of the solutions z′ (depicted in Fig. (1)) consists of (compositions of) the reflections (21) acting on the sides (19) of the system and tiles the Poincar´e Plane uniformly.
This choice comprehends the action of the operators T1 and T2 on different geodesics in (24), and, in particular, on those for which 0 ≤ x ≤ 1. Furthermore, the interval [0,1] is this way piecewise sent to different intervals of the real axes by T3.
The folding group for periodic geodesics consists of the action of the operators T1, T2, and T3 according to the periodic solutions of (24) and does not tile the Poincar´e Plane completely.
Corollary 6. The number F(ni) corresponds to the (ni) − th digit of the continued fraction expansion of the surd. The extraction of such a digit is consistent with recognizing the corresponding discrete map, as examined for more general cases by R. Adler, L. Flatto, and G.C Layek [10, 1], respectively. A different choice for the definition of the oriented endpoints, as, i.e. those chosen by E.B. Bogomolny, B. Georgeot, M.-J. Giannoni, C. Schmit, or those preferred by C. Series [23, 3], resp., does not allow for this construction for Hamiltonian systems.
The correspondence (24) allows one to use the results of C. Series [4], in which the succession of digits in a continued fraction decomposition can be understood to better follow the Gauss-Kuzmin distribution rather than that of a Markoff chain analysis of the corresponding (stochastized) process. The Γ2 subgroup is defined according to the first two iterations of (24), for which it is not relevant to know whether the corresponding geodesics is rational or irrational, and, in case, the pattern of digits according to which the definition of ’irrational’ is further specified, i.e. whether periodic or not.
In the study by C. Series [4], the free group F on a torus is defined as consisting of a translation (resulting from the composition of two reflections, such as (21) and (22) in (21)) and an inversion with respect to a circumference (such as (23) in (21)). The definition of periodic geodesics by setting z′ = z in (24) allows one to apply the Gauss-Kuzmin theorem to the (therefore so-called) ’surds’ geodesics, whose classification is ’reduced’ as their endpoint(s) are (equivalently)defined within the unit interval. The definition of ’cutting’ is consistent with that defining the subgroup leaving invariant the corresponding Hamiltonian problem, for which no operator can be composed with its inverse (even though such composition exists in the original bigger group).
As a new result, considering the Hamiltonian problem allows one to further classify the geodesics by choosing an orientation, i.e. by labelling the endpoints x and x′ according to the Γ2 subgroup. Furthermore, the ’cutting’ (Γ2 congruence sub-) group (associated to a Hamiltonian problem) allows one to chose an orientation for endpoints, such that the same non-oriented geodesics are established to be classified as different cutting geodesics for the problem studied by C. Series [4], according to the different classification the (naturally) occupy within the initial conditions of the Hamiltonian problem which is defined.
Differently from the analyses by G.A. Hedlund [22], considering the solution of a Hamiltonian problem does not require to take into account the metric transitivity of the (composition of) transformation(s). The metric transitivity is nevertheless still important in the comparison of the folding group with the tiling group, and in establishing which folding group(s) are not accepted as a tiling group, (as it will be discussed in section ’Different systems’). As examined by E. Gutkin and B. Gruenbaum [24, 25], resp., Fano orbits are demonstrated to be ruled out in Hyperbolic geometry, the classification of ’oriented’ geodesics needs one to abandon the comparison with Euclidean geometry investigated by C. Series [4], for the presence of periodic orbits. Such a comparison is nevertheless useful for the analysis of the role of the presence of the absolute (i.e. the boundary of the Poincar´e plane, which consists of the horizontal axis and one point at v = ∞) in the domain of generalized triangles and the corresponding ’punctures’ on the tori, which are constructed as their congruence subgroups, are generated by the effects on the folding acted by the digit distribution in the continued-fraction expansion of the (’Hamiltonianly’-)selected oriented endpoints of trajectories which ly close to rational trajectories.
The exclusion of points from the sides of a domain can also be considered even if the shape of the domain does not comprehend the absolute; indeed, in examinations by I.P. Cornfeld, S.V. Fomin and Ya.G. Sinai [26], nondifferentiable points are excluded from the domain enclosing a chaotic dynamics resulting from a Hamiltonian system, even though these points do not belong to the absolute (i.e. but are the corners of a polygon).
5. RATIONAL GEODESICS
It is now possible to classify the possibility of occurrence of geodesics parameterized by one endpoint belonging to the absolute within a continuous, not differentiable point of the potential shape (corner).
Within the Hamiltonian approach, the ’forward’ (+) endpoint of such geodesics is a rational number (on the real axis), whose continuous-fraction expansion is finite.
Theorem 7. For the system PGL(2,C) rational geodesics exist.
Proof 8.− Any rational trajectories for the domain (19) are those such that x− = ∞, x+ ϵ [−1/2,0], or x+ = ∞, x ϵ [−1/2,0], i.e. degenerate geodesics with u = const, u−ϵ ∆[−1/2,0], ∀v ϵ (19), and those transformed by elements of the group into x+ = ∞ geodesics, the value of− x represented by a continued fraction with one digit, 1/x−. Transformations able to send geodesics into x = ∞ geodesics do not belong to the group (trivial/vanishing definition of the denominator).
For the congruence subgroups of PGL(2,C) rational geodesics exist.
Theorem 9. For the congruence subgroups of PGL(2,C) defined on domains containing one point at the absolute v = ∞, rational geodesics are those parameterized by the condition [cfr. Th. 3]− x− = ∞, x+ in the abscissa interval on which the (sub)group domain is defined, or x+ = ∞, x in the abscissa interval on which the (sub)group domain is defined, and those so-transformed by the evolution of the equations of motion.
Theorem 10. For the congruence subgroups of PGL(2,C) defined on domains containing more than one point ui on the absolute at v = 0, rational geodesics are the degenerate geodesics with x± = ui, (i.e. u = const = ui), and the non-degenerate geodesics with x± = ui, the other endpoint parameterized such that the intersection with the group domain is not at v = 0 (the u axes), and those so transformed by the evolution of the equations of motion (in both cases, respectively).
For larger domains, obtained as congruence subgroups of PGL(2,C), the set of values parameterizing rational geodesics is one defining rational geodesics for the cases in Theorem 9 and Theorem 10, and those for which the cases of Theorem 10 are predicted by the evolution of the equations of motion. Such larger domains can be understood as particular (arbitrary) truncations of the tiling resulting from the folding of a trajectory in a (most generally, asymmetric) triangle.
6. TORI
Tori are obtained as the tiling resulting from the folding of particular orbits of triangles. For the folding of irrational non periodic geodesics in the domain (19) of the PGL(2,C) group, no particular geodesics have to be chosen for the obtainment of a torus.
Defining tori by their rational geodesics is allowed as by the investigation by G.A. Hedlund [22], where tori have been commented to be metrically invariant under a smaller group (the modular group), as well as their rational geodesics; this approach to the problem is opposite to that proposed by the applications by C. Series [4], as far as the definition of kinds of the torus is concerned: it rather follows Series’ suggestion about the research guidelines specified by G.A. Hedlund [27].
The invariance of the rational geodesics of tori under the action of the modular group allows one to describe punctured tori as well.
Their derivation is here achieved with respect to the PGL(2,C) group for the dynamical problem associated.
Definition 11. Tori are obtained as the limiting (with respect to the absolute) tiling resulting from the folding of particular orbits, (for example, irrational geodesics).
Differently, ’punctured’ tori are obtained as the tiling resulting from the folding of particular orbits (for example, rational ones and periodic ones).
Remark 12. By means of the action of the PGL(2,C) group on Hamiltonian systems, there is a one-to-one correspondence (by construction) on the orbits in the triangle and the orbits in the tori of which they are the evolution of the folding. The converse is not true.
Because of the hyperbolic geometry, no ’horizontal’ tori can be (at least geodesically) defined.
It is indeed possible to define Hamiltonian systems whose potential is defined by two degenerate (straight lines) geodesics. Within the present approach, such a construction coincides with the limn→∞ Γ2n congruence subgroup of PGL(2,C), i.e. with the tessellation of the domain u ϵ ∆x, ∀v according to the reflection with respect to a circumference of the considered PGL(2,C) group. If the limit is not achieved, a (degenerate) ’punctured torus’ is obtained (Fig. (2)), similarly to the constructions by C. Series [4].
Theorem 13. Rational geodesics for the Hamiltonian system associated with the limiting process of tessellation of a (degenerate) torus are any geodesics for which x+ ϵ ∆x, or x− ϵ ∆x on the torus.
Corollary 14. (Non-degenerate) Rational geodesics for the (degenerate) torus, are geodesics with one oriented endpoint coinciding with any point on the absolute of the domain, and intersecting the torus domain at a different point, for which v = 0.6
Corollary 15. Degenerate rational geodesics for the (degenerate) torus are those with one endpoint coinciding with any point on the absolute of the domain, and the other at ∞.
The initial conditions also define the allowed orientation for the solutions of the equations of motion.
Theorem 16. Rational geodesics for the Hamiltonian system associated with the limiting process of tessellation of a (non-degenerate) torus are any geodesics with x+ = χ+ and x− on the potential sides; such a case is within the allowed initial conditions of the problem.
Corollary 17. (Non-degenerate) Rational geodesics for the (non-degenerate) torus are geodesics with one oriented endpoint coinciding with any point on the absolute of the domain of the potential shape, and intersecting the torus domain at a different point, for which v = 0.6
Corollary 18. Degenerate rational geodesics for the (non-degenerate) torus are allowed as initial conditions; the corresponding geometrical construction is a (degenerate) geodesics having in common with the potential only one point on the absolute and one on the potential side corresponding to the same abscissa.
7. PUNCTURED TORI
Definition 19. ’Punctured’ tori are obtained as the tiling resulting from the folding of particular orbits (for example, rational ones and periodic ones).
Theorem 20. Rational geodesics for the Hamiltonian system associated with the limiting process of tessellation of a (degenerate) ’punctured’ torus are any geodesics for which x+ ϵ ∆x, or x− ϵ ∆x on the (’punctured’) torus.
Corollary 21. (Non-degenerate) rational geodesics for the (degenerate) ’punctured’ torus are geodesics with one oriented endpoint coinciding with any point on the absolute of the domain of the (degenerate) ’punctured’ torus, and intersecting the torus domain at a different point, for which v = 0.6
Corollary 22. Degenerate rational geodesics for the (degenerate) ’punctured’ torus are those with one endpoint coinciding with any point on the absolute of the domain of the (degenerate) ’punctured’ torus, and the other at ∞.
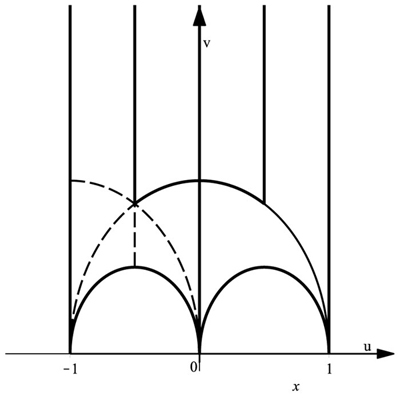
A further generalization of the material in the above is the definition of a Hamiltonian system whose potential is defined by two (non-degenerate) geodesics with one common endpoint (χ+), the other endpoint defining an interval ∆x non containing the common endpoint. This shape is interpreted as the limiting tessellation iteration of a Γ2 congruence subgroup of PGL(2,C). The non-limiting (tessellation) process provides on with a (non-degenerate) ’punctured torus’ (Fig. (3).
Theorem 23. Rational geodesics for the Hamiltonian system associated with the limiting process of tessellation of a (non-degenerate) punctured torus are any geodesics with x+ = χ+ or x− on the potential sides; such a case is within the allowed initial conditions of the problem.
Corollary 24. (Non-degenerate) Rational geodesics for the (non-degenerate) ’punctured’ torus are geodesics with one oriented endpoint coinciding with any point on the absolute of the domain of the potential shape, and intersecting the torus domain at a different point, for which v = 0.6
Corollary 25. Degenerate rational geodesics for the (non-degenerate) ’punctured’ torus are allowed as initial conditions; the corresponding geometrical construction is a (degenerate) geodesics with one endpoint on the absolute.
Remark 26. The existence of such geodesics notwithstanding, not all the corresponding solutions of the equation of motion are allowed by the initial conditions. It is indeed possible to define such rational geodesics also outside the potential of the system (for which the need for the specification of the intersection with the potential sides not to be on the absolute).
Degenerate ’punctured’ tori can be identified in Fig. (3): they are delimited by two degenerate (’vertical’) geodesics and one (non-degenerate) circumference with the two endpoints in common with the other two vertical geodesics. Non-degenerate ’punctured’ tori are also described in Fig. (3); they are closed domains delimited by three half circumferences having in common one endpoint with each other.
8. DIFFERENT SYSTEMS
It is interesting to analyze different systems, for which discrepancies can be outlined.
Any group smaller than PGL(2,C), as defined by A. Terras and employed by C. Series [2, 4], resp., can be described on the corresponding domain also used in [2] as a suitable congruence subgroup of it, as studied, i.e., by N.I. Koblitz [6].
Because the associated chaotic system is Hamiltonian, it is indeed easy to verify that the evolution of the geodesics z′ (24) is continuous. For this problem, not all sequences of operators in (24) are comprehended, even though they are allowed by (21), and, in particular, by (21), which is usually taken as on of the two transformations (different from one on a non-degenerate geodesics), which defines the folding group for the discrete map associated to the dynamical system.
The modular group SL(2,Z) is defined by the reflections Ta, Tb, Tc, s.t.
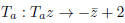 |
(24) |
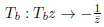 |
(25) |
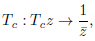 |
(26) |
on the domain 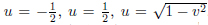 . For the symmetric domain of the modular group, the folding group [28] does not correspond to the tiling group [3], as the translation z → z − 1 does not compose consistently with the reflection with respect to (”on”) the geodesics x2 + y2 = 1.
. For the symmetric domain of the modular group, the folding group [28] does not correspond to the tiling group [3], as the translation z → z − 1 does not compose consistently with the reflection with respect to (”on”) the geodesics x2 + y2 = 1.
The inadequacy of the folding group to provide with a suitable tiling of the Poincar´e Plane for this construction has also been outlined in [11] for the group PSL(2,R), for the solution of the corresponding Hamiltonian system, as examined by R. Adler and L. Flatto [10], was proposed by D. Fried [12]. In particular, the translation defining SL(2,R) in E.B. Bogomolny [28] does not imply the reflections needed for the folding to be also a tiling, the high symmetry of the problem not with standing.
The subgroup Γ0 of PGL(2,C) on the domain delimited as 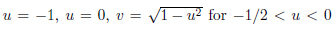 and
and 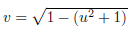 by the transformations
by the transformations
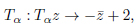 |
(27) |
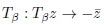 |
(28) |
and by the reflections on the two circumferences. This subgroup, smaller than PGL(2,C), is different from one constructed from SL(2,Z), as it is not consistent with the reflection 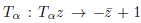 of PGL(2,C). For this symmetric domain of PGL(2,C), the folding group does not correspond to the tiling group.
of PGL(2,C). For this symmetric domain of PGL(2,C), the folding group does not correspond to the tiling group.
Any group smaller than PGL(2,C), studied also by A. Terras in [2], can be described on the corresponding domain, as pertinently outlined by A. Terras in [2], as a suitable congruence subgroup of it, as reported, i.e., by N.I. Koblitz [6].
Because the associated chaotic system is Hamiltonian, it is indeed easy to verify that the evolution of the geodesics z′ (24) is continuous. For this problem, not all sequences of operators in (24) are comprehended, even though they are allowed by (21), and, in particular, by (21), which is usually taken as on of the two transformations (different from one on a non-degenerate geodesics), which defines the folding group for the discrete map associated to the dynamical system.
The modular group SL(2,Z) is defined by the translations 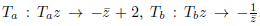 , on the domain
, on the domain 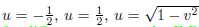 . For the symmetric domain of the modular group, the folding group, as investigated, for different purposes, by E.B. Bogomolny [28], does not correspond to the tiling group individuated by C. Series [3], as the translation z → z − 1 does not compose consistently with the reflection with respect to (”on”) the geodesics x2 + y2 = 1.
. For the symmetric domain of the modular group, the folding group, as investigated, for different purposes, by E.B. Bogomolny [28], does not correspond to the tiling group individuated by C. Series [3], as the translation z → z − 1 does not compose consistently with the reflection with respect to (”on”) the geodesics x2 + y2 = 1.
The inadequacy of the folding group to provide with a suitable tiling of the Poincar´e Plane for this construction has also been outlined by D. Mayer and F. Stroemberg [11], for the group PSL(2,R), for the solution of the corresponding Hamiltonian system studied by R. Adler and L. Flatto [10], was proposed by D. Fried [12]. In particular, the translation defining SL(2,R), as outlined, for a different Hamiltonian application, by E.B. Bogomolny [28], does not imply the reflections needed for the folding to be also a tiling, the high symmetry of the problem notwithstanding.
The subgroup Γ0 of PGL(2,C) on the domain delimited as u = −1, u = 0, v = √1 − u2 for −1/2 < u < 0
and v = p1 − (u2 + 1) and by the transformations 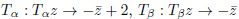 and by the reflections on the two circumferences. This subgroup, smaller than PGL(2,C), is different from one constructed from SL(2,Z), as it is not consistent with the reflection Tα : Tαz → −z¯ + 1 of PGL(2,C). For this symmetric domain of PGL(2,C), the folding group does not correspond to the tiling group.
and by the reflections on the two circumferences. This subgroup, smaller than PGL(2,C), is different from one constructed from SL(2,Z), as it is not consistent with the reflection Tα : Tαz → −z¯ + 1 of PGL(2,C). For this symmetric domain of PGL(2,C), the folding group does not correspond to the tiling group.
The definition in Th. 5.23 in enunciated by C. Series [3], applies to a Hamiltonian system whose potential is consistent with a congruence subgroup Γ2 of PGL(2,C) which leaves invariant the solutions of a Hamiltonian system whose potential is specified as containing at least one point in the interval −1 < x < 1. Four realizations of this (sub)group can be outlined in Fig. (3).
The occurrence of rational geodesics in dynamical systems on tori is characterized here for dynamical systems as for their (Hamiltonian-time) irreversibility; their geometrical occurrence declares a set of initial conditions, similarly to the cases studied By G.A Hedlund [29], which is outlined, the metric transitivity of the manifold remaining unchanged.
Non-arithmetical triangles, i.e. those triangles whose angles define a domain for a non-arithmetical group, as in the study by W. Barth, C. Peters and A. Van de Ven, B.N. Apanasov and E.B. Bogomolny, C. Schmit [30, 32] need different definitions for the tiling of tori, and will not be analyzed here.
9. RESULTS
In the present paper, Hamiltonian systems (whose potential is) associated with the group PGL(2,C) ant its congruence subgroups have been analyzed. A definition for reduced quadratic surds has been proposed for the Gauss-Kuzmin Theorem to apply for the geodesics of the problem. This method allows for the analysis of the definition of the allowed initial conditions, and, therefore, for the classifications of the orbits of the system. The use of the group PGL(2,C) and its congruence subgroups is the only one valid in defining the folding group for the system as the tiling group for the Poincar´e Plane.
CONCLUSION
In a study [33] by M. Henneaux and C. Teitelboim, the quantization of gauge systems is analyzed for constrained Hamiltonian systems.
The Lagrangean for the motion of a particle of unitary mass without potential on the upper Poincar´e half plane is given as
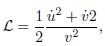 |
(29) |
where the Lagrangian variables are this way defined. Outside the group domain, the Lagrangian reads
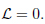 |
(30) |
The quantization of the case of the Lagrangians in the present analysis, i.e. 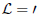 (topological classical mechanics) and
(topological classical mechanics) and 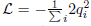 , where the Lagrangians variables qi form the upper Poincar´e half plane are defined in Eq. (30). In the present work, the case L = 0 (which applies in the regions of the hyperbolic plane outside the subgroups domains and the group domains) is not invariant under arbitrary shifts of the variables qi. For the case
, where the Lagrangians variables qi form the upper Poincar´e half plane are defined in Eq. (30). In the present work, the case L = 0 (which applies in the regions of the hyperbolic plane outside the subgroups domains and the group domains) is not invariant under arbitrary shifts of the variables qi. For the case 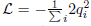 , which applies in the regions of the hyperbolic plane inside the subgroups domains and the group domains, the Lagrangian is not invariant under arbitrary shifts, but only to those defined by each group under consideration, i.e. u → u + λ.
, which applies in the regions of the hyperbolic plane inside the subgroups domains and the group domains, the Lagrangian is not invariant under arbitrary shifts, but only to those defined by each group under consideration, i.e. u → u + λ.
The phase space associated is indeed one with unitary geodesics velocities.
The primary constraints 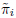 = 0, for the Hamiltonians
= 0, for the Hamiltonians 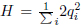 are defined for the class of transformations (i.e.
are defined for the class of transformations (i.e.
for the groups) under consideration. The secondary constraints are 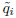 = 0. The constraints
= 0. The constraints 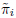 = 0 and
= 0 and 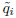 = 0 both second-class constraints. Upon gauge fixation, they are equivalent to the first-class constraint
= 0 both second-class constraints. Upon gauge fixation, they are equivalent to the first-class constraint 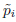 = 0. The constraint
= 0. The constraint 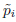 = 0 cannot be interpreted as a gauge-fixing condition, as the Lagrangian L = 0 is not invariant under arbitrary shifts of the variables qi. The gauge is completely fixed by
= 0 cannot be interpreted as a gauge-fixing condition, as the Lagrangian L = 0 is not invariant under arbitrary shifts of the variables qi. The gauge is completely fixed by 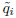 = 0; by means of unfreezing th degrees of freedom of the gauge
= 0; by means of unfreezing th degrees of freedom of the gauge 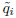 = 0, the same constrained Hamiltonian system is recovered.
= 0, the same constrained Hamiltonian system is recovered.
The constraints structure can also be analyzed for the transformations (22) and (23) in (21).
Given a phase space with constraints by J. Stasheff [34], by means of the symplectic structure, they correspond to Hamiltonian vector fields tangent to the constraint surface and foliating the constraint surface, the zero locus of the constraints. Ghosts, i.e. Grassmann algebra generators, can be added to the Poisson algebra of the so-obtained reduced phase space, endowed with a complex structure, to the Poisson algebra of the smooth functions of the original phase space, as demonstrated by E.S. Fradkin and G.S. Vilkovisky [35].
A foliation procedure can also be applied to the coordinate space of General Relativity (within the thin-sandwich conjecture under the hypothesis of the Geroch theorem), and the corresponding constraints formalism can be applied to phase space resulting from the Hamiltonian expression for General Relativity [36], as formulated by R. L. Arnowitt, S. Deser and C. W. Misner. In the canonical form, the Dirac algebra of the constraints can be formulated in terms of Lagrange multipliers in the phase space. In particular, the scalar constraint, the vector constraint and the momenta constraint are implemented.
For a Hassan-Rosen theory of gravity, it is possible to introduce an interaction terms such as V ((g−1f)n) or
V ((pg−1f)n), with the external metric fµν, as in the model analyzed by Z. Molaee and A. Shirzad [37]. For the bi-gravity theory to be ghost free, the interaction terms have to be diffeomorphism-invariant, its derivatives w.r.t to the lapse functions and the shift function must obey suitable conditions, and the corresponding constraint must not contain lapse functions and shift functions. The Hassan-Rosen bimetric theory of gravity has been shown to be a ghosts-free, as outlined by S. F. Hassan and R. A. Rosen [38].
Three-gravity has been studied by M. Sadegh and A. Shirzad [39], for which 2 of the 6 components of the metric are found to be dynamical. The corresponding st of constraints is analyzed. Constraints for three-dimensional gravity are found. A 6-member family of second class constraints is analyzed to correspond to a family of 24-member, 2-level and cross-conjugate second class system, a one-level 12-member family of second class constraints, an 8-member 2-level family of second class constraints and a 6-member family of second class constraints gathered in three-level chains, a 6-member, 2-level and first class family of constraints (which correspond to 6 first- class constraints. As a result, 36 primary and 26 secondary constraints are found, of which 56 are second-class and 6 are first-class.
Three-gravity theories and for four-gravity theories in the Hamiltonian formalisms in the ADM decomposition where studied by Z. Molaee and A. Shirzad [40]. Within the framework of the ADM decomposition of the phase space, diffeomorphisms-invariance is assured by first -class constraints, and second-class constraints to avoid ghost-fields are found.
Among other maps considered for the continued-fraction expansion for the geodesics of the fundamental domain for the Upper Poincar´e Half Plane, the Lehner map L Eq. (2) can also be compared with (inequivalent) the Farey-Isola map, LFI, formulated by S. Isola [41], defined on the interval [0,1] as
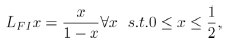 |
(31) |
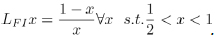 |
(32) |
While the Gauss map and and the Farey-Isola map are inequivalent, their generalized Borel transforms and Laplace transforms are left invariant under the definitions of transfer operators as calculated by V. Baladi and P. Collet [42, 43], resp.
A definition for reduced geodesics for the group PGL(2,C) on the Upper Poincar´e Half Plane has been provided for the sake of classification of solution to the free Hamiltonian problem implemented on the fundamental domain of the group PGL(2,C); such a classification has implied the necessity to discard the symmetry SL(2,Z). The properties of the group PGL(2,C) on the Upper Poincar´e Half Plane allow for the classification of points and geodesics within it fundamental domain. The classification of geodesics provides one with the tools for new construction of tori and of punctured tori on the Upper Poincar´e Half Plane (for the group PGL (2,C)). The properties of the geodesics for the group PGL(2,C) also allow for new definitions of tessellation for the Upper Poincar´e Half Plane.
The study of different groups in hyperbolic geometry for the Upper Poincar´e Half Plane might allow for a new classification of points, geodesics, tori, and tessellations for the considered groups. The corresponding free Hamiltonian problems lead to the proper definition of reduced geodesics to obtain the classification of points and gain insight on the dynamics. The definition of the reduced continued fraction can, therefore, lead to new kinds of tesselation for the Upper Poincar´e Half Plane and for new construction of tori and/or generalized tori.
In particular, the study of non-arithmetic groups is expected to lead to the finding of new structures and new results, as considered by E.B. Bogomolny, M. Georgeot, M.-J.Giannoni ad C.Schmit [23]. The paper has been organized as follows.
In Section II, geodesics and their corresponding continued fraction-expressions are revised for several groups on the Upper Poincar´e Half Plane. Examples of classifications of points are also recalled.
In Section III, generalized triangles have been reminded of the Poincar´e Plane.
In Section IV, equations of motions (as the solution for Hamiltonian systems) have been investigated to be continued under the action of the group PGL(2,C), which defines a way to classify geodesics by applying the Gauss-Kuzmin Theorem to their ’reduced’ definition.
In Section V, the solutions to the equations of motions have been classified w.r.t the comparison with the tesselation techniques for the hyperbolic plane.
In Section VI, tori and their geodesics have been defined according to the hints of [3] for the Γ2 congruence subgroups of PGL(2,C).
In Section VII, the construction of punctured tori is considered as from the folding of rational trajectories and periodic ones.
In Section VIII, different systems have been analyzed for comparison, in which the tiling group for the Poincar´e Plane does not correspond to the folding group of the associated Hamiltonian system.
OML would like to thank Roberto Conti for useful comments, and Pavol Zlatos’ for reading the manuscript. OML is grateful to the Referees for having pointed out Ref.’s [33, 37, 36, 39, 40].
Four realizations of Γ2 of PGL(2,C) can be recognized in the picture, i.e. those whose operators imply reflections on the following (close) set of sides: 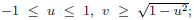
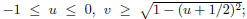
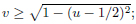
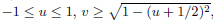
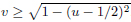 .
.
It is interesting to remark here that the group PGL(2, Z) is not sufficient to provide with all these constructions.
Two limiting processes for the punctured torus are also recognized, i.e. for the degenerate punctured torus, delimited by any two degenerate geodesics (vertical lines), and for the non-degenerate punctured torus, delimited by two circumferences having one point in common and defining an interval ∆x comprehended by the two other non-coinciding endpoints on the
the same portion of the real axes wrt the common one, such as, for example, u = 1, v = √1 − u2 and v = √u − u2.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
Not applicable.
FUNDING
None.
CONFLICT OF INTEREST
The author declares no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
OML is grateful to Hermann Nicolai for outlining the relevance of Ref. [23].
REFERENCES
| [1] | Layek GC. An Introduction to Dynamical Systems and Chaos 2015. |
| [2] | Harmonic Analysis on Symmetric Spaces and Applications 1985. |
| [3] | Series C. Geometrical methods of symbolic coding. In: Bedford T, Keane M, Series C, Eds. Ergodic Theory and Symbolic Dynamics in Hyperbolic Spaces 1991; 125-51. |
| [4] | Series C. The geometry of Markoff numbers. Math Intell 1985; 7: 20-9. |
| [5] | Series C. Symbolic Dynamics for Geodesic Flows In: Gleason AM, Ed. Proceedings of the International Congress of Mathematicians 1210-52.Berkeley, California, USA. 1986; pp. 1986; |
| [6] | Koblitz NI. Introduction to Elliptic Curves and Modular Forms 1993. |
| [7] | Miller SJ, Takloo-Bighash R. An Invitation to Modern Number Theory 2006. |
| [8] | Hardy GH. Quadratic Surds 10th ed. 1967. |
| [9] | Aicardi F. Symmetries of quadratic forms classes and of quadratic surds continued fractions Part II: Classification of the periods’ palindromes pre-print arXiv:0708.2082. |
| [10] | Adler R, Flatto L. Cross section maps for the geodesic flow on the modular surface”, Contemp. Math. Conference on Modern Analysis and Probability vol. 26: 9-24.Providence, R.I.. 1984; pp. 1984; |
| [11] | Mayer D, Stroemberg F. Symbolic dynamics for the geodesic flow on Hecke surfaces Journal of Modern Dynamics 2008; 2: 581-627. pre-print arXiv:0801.3951 |
| [12] | Fried D. Symbolic dynamics for triangle groups. Invent Math 1996; 125: 487-521. |
| [13] | Lecian O M. Modular structures and extended-modular-group-structures after Hecke pairs J Phys Conf Series 2019; 1194(1-11): 012067. |
| [14] | Atkin AOL, Lehner J. Hecke operators on Γ0(m). Math Ann 1970; 185: 134-60. |
| [15] | Lehner J. Semiregular Continued Fractions whose Partial Denominators are 1 or 2”, The Mathematical Legacy of Wilhelm Magnus: Groups, Geometry, and Special Functions Conference on the Legacy of Wilhelm Magnus May 1-3, 1992; Brooklyn, NY. 1994.1994. |
| [16] | Dajani K, Kraaikamp C. The Mother of All Continued Fractions pre-print http://www.math.uu.nl/publications/preprints/1106 |
| [17] | Rosen D. A class of continued fractions associated with certain properly discontinuous groups. Duke Math J 1954; 21: 549-63. |
| [18] | Rosen D, Schmidt TA. Hecke groups and continued fractions. Bull Aust Math Soc 1992; 46: 459-74. |
| [19] | Schmidt TA, Sheingorn M. Length spectra of the Hecke triangle groups. Math Z 1995; 220: 369-97. |
| [20] | Schmidt TA. Remarks on the Rosen lambda-Continued Fractions”, Number theory with an emphasis on the Markoff spectrum (Provo, UT, 1991), Series: Lecture Notes in Pure and Appl Math, A Pollington and W Moran Ed’s 1993; Vol. 147: 227-38. |
| [21] | Schmidt TA, Sheingorn M. Covering the Hecke Triangle Surfaces. Ramanujan J 1997; 1: 155-63. |
| [22] | Hedlund GA. On the Metrical Transitivity of the Geodesics on Closed Surfaces of Constant Negative Curvature. Annals of Mathematics, Second Series 1934; 35: 787-808. |
| [23] | Bogomolny EB, Georgeot B, Giannoni M-J, Schmit C. Arithmetical chaos Physics Reports 1997; 291: 219-324. |
| [24] | Gutkin E. Billiards in polygons Physica 1986; D 19: 311-33. |
| [25] | Gruenbaum B. Configurations of Points and Lines 2009. |
| [26] | Cornfeld IP, Fomin SV, Sinai YaG. Ergodic Theory 1982. |
| [27] | Hedlund GA. A Metrically Transitive Group Defined by the Modular Group. Am J Math 1935; 57: 668-78. |
| [28] | Bogomolny EB. Quantum and Arithmetical Chaos pre-print arXiv:nlin/0312061 |
| [29] | Hedlund GA. The dynamics of geodesic flows. Bull Am Math Soc 1939; 45: 241-60. |
| [30] | Barth W, Peters C, van de Ven A. Compact Complex Surfaces 2004. |
| [31] | Apanasov BN. Conformal Geometry of Discrete Groups and Manifolds 2011. |
| [32] | Bogomolny EB, Schmit C. Multiplicities of Periodic Orbit Lengths for Non-Arithmetic Models. J Phys A 2004; 37: 4501-38. |
| [33] | Henneaux M, Teitelboim C. Quantization of gauge systems 1992. |
| [34] | Stasheff J. Homological (ghost) approach to constrained Hamiltonian systems pre-print hep-th/9112002 |
| [35] | Fradkin ES, Vilkovisky GS. Quantization of relativistic systems with constraints. Phys Lett B 1975; 55: 224-6. |
| [36] | Arnowitt RL, Deser S, Misner CW. The Dynamics of general relativity. Gen Relativ Gravit 2008; 40: 1997-2027. [pre-print]. |
| [37] | Molaee Z, Shirzad A. Hamiltonian structure of bi-gravity, problem of ghost and bifurcationClass Quant Grav 2019; 36: 225005-26. [arXiv:1805.02179 [hep-th]]. |
| [38] | Hassan S F, Rosen R A. Bimetric Gravity from Ghost-free Massive Gravity JHEP 2012; 126: 02-14. |
| [39] | Sadegh M, Shirzad A. Constraint strucrure of the three dimensional massive gravity.Phys Rev D 2011; 83: 084040-048. |
| [40] | Molaee Z, Shirzad A. Hamiltonian formalism of the ghost free Tri(-Multi)gravity theory pre-print arXiv:1908.05041 [hep-th].. 1908. |
| [41] | Isola S. On the spectrum of Farey and Gauss mapsNonlinearity 2002; 15: 1521-39. |
| [42] | Baladi V. Positive Transfer Operators and Decay of Correlations 2000. |
| [43] | Collet P. Some ergodic properties of maps of the interval”, Dynamical Systems, proceedings of the first UNESCO CIMPA school of Dynamics and disordered systems (Temuco, Chile, 1991) 1996. |